Linéarité de l'intégrale
Théorème :
Soient \(f\) et \(g\) deux fonctions continues sur un intervalle \(I\). Soit \(\alpha\) un réel quelconque, \(a\) et \(b\) deux éléments de \(I\).
\(\displaystyle \int_{a}^{b}[f\left(t\right)+g\left(t\right)]\mathrm{d}t=\int_{a}^{b}f\left(t\right)\mathrm{d}t+\int_{a}^{b}g\left(t\right)\mathrm{d}t\)
\(\displaystyle \int_{a}^{b}\alpha f\left(t\right)\mathrm{d}t=\alpha\int_{a}^{b}f\left(t\right)\mathrm{d}t\)
Exemple :
Soit \(A=\displaystyle \int_{0}^{1}\mathrm{d}x\), \(B=\displaystyle \int_{0}^{1}x\mathrm{d}x\) et \(C=\displaystyle \int_{0}^{1}x^{2}\mathrm{d}x\). Caculons en fonction de \(A\), \(B\) et \(C\) les intégrales suivantes :
\(I=\displaystyle \int_{0}^{1}\left(3x^{2}-4x+5\right)\mathrm{d}x\)
\(J=\displaystyle \int_{-1}^{1}\left(x^{2}-3x+8\right)\mathrm{d}x\)
Puis, nous calculerons \(I\) et \(J\) (on admettra que \(C=\frac13\)).
\(I=\displaystyle \int_{0}^{1}\left(3x^{2}-4x+5\right)\mathrm{d}x\)
Par linéarité de l'intégrale, \(I=3\displaystyle \int_{0}^{1}x^{2}\mathrm{d}x-4\int_{0}^{1}x\mathrm{d}x+5\int_{0}^{1}\mathrm{d}x\).
Donc \(I=3C-4B+5A\).
De même, \(J=C-3B+8A\).
Calcul de A
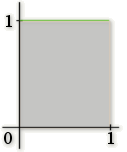
\(A\) est l'aire en unité d'aire du rectangle grisé ci-contre.
Donc \(A = 1\).
Calcul de B
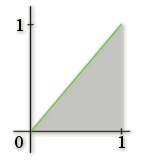
\(B\) est l'aire en unité d'aire du triangle grisé ci-contre.
Donc \(B=\dfrac{1\times1}2=\dfrac12\).
Calcul de C
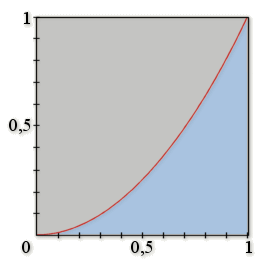
\(C\) est l'aire en unité d'aire sous la parabole.
On justifiera ultérieurement (partie sur les primitives) que \(C=\dfrac13\).
Donc \(I=4\) et \(J=\dfrac{41}6\).