Extension à une fonction continue sur un intervalle et de signe quelconque
Définition :
Soit \(f\) une fonction continue sur \([a;b]\) avec \(a\leqslant b\).
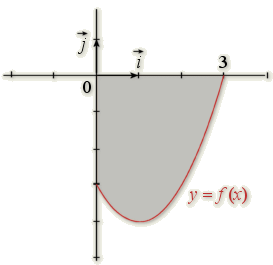
Si \(f\) est négative sur \( [a;b]\), \(\displaystyle \int_{a}^{b}f\left(t\right)\mathrm{d}t=-\mathrm{aire}\left(D\right)\).
Dans le graphique ci contre, \(D\) est représenté par la partie grisée, \(a = 0\) et \(b = 3\).
\(\displaystyle \mathrm{aire}\left(D\right)=-\int_{0}^{3}f\left(t\right)\mathrm{d}t\)
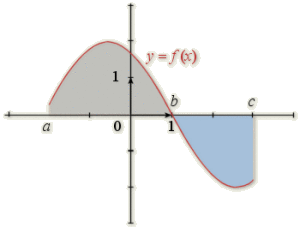
Si \(f\) est de signe quelconque :
\(D_1\) est représenté par la partie grisée.
\(D_2\) est représenté par la partie bleutée.
\(\begin{array}{rcl} {\displaystyle \int_{a}^{c}f\left(t\right)\mathrm{d}t} &=&aire\left(D_1\right) - aire \left( D_2 \right) \\ &=&{\displaystyle \int_{a}^{b}f\left(t\right)\mathrm{d}t+\displaystyle \int_{b}^{c}f\left(t\right)\mathrm{d}t } \end{array}\)