Cas d'une fonction positive continue sur un intervalle fermé
Définition :
Le plan est rapporté à un repère orthogonal \(\left(O;\vec{\imath} , \vec{\jmath}\right)\). Soient \(I\) et \(J\) les points tels que \(\overrightarrow{OI}=\vec \imath\) et \(\overrightarrow{OJ}=\vec{{j}}\). On définit l'unité d'aire comme étant l'aire du rectangle construit avec les points \(O\), \(I\) et \(J\).
Le plan est rapporté à un repère orthogonal \(\left(O;\vec{\imath} , \vec{\jmath}\right)\). Soient \(I\) et \(J\) les points tels que \(\overrightarrow{OI}=\vec \imath\) et \(\overrightarrow{OJ}=\vec{{j}}\). On définit l'unité d'aire comme étant l'aire du rectangle construit avec les points \(O\), \(I\) et \(J\).
Soit \(f\) une fonction continue et positive sur un intervalle \(I\), \(\mathcal C\) sa courbe représentative dans un repère orthogonal, \(a\) et \(b\) deux éléments de \(I\) tels que \(a\leqslant b\). Soit \(D\) la partie du plan délimitée par la courbe \(\mathcal C\), l'axe des abscisses et les droites d'équations respectives \(x = a\) et \(x = b\).
L'aire, en unités d'aire, de \(D\), est appelée intégrale de \(a\) à \(b\) de \(f\).
Cette intégrale se note \(\displaystyle \int_{a}^{b}f\left(t\right)\mathrm{d}t\).
Les réels \(a\) et \(b\) sont appelés les bornes de l'intégrale.
\(\displaystyle \int_{a}^{b}f\left(t\right)\mathrm{d}t\) ne dépend pas de la lettre \(t\) ; la lettre \(t\) est une variable muette. Elle peut être remplacée par n'importe quelle autre lettre.
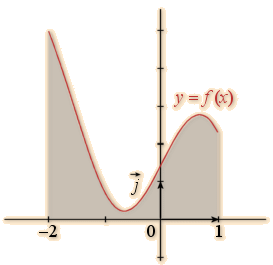
Dans le graphique ci dessous, \(D\) est représenté par la partie grisée, \(a = -2\) et \(b = 1\) : \(\displaystyle \mathrm{aire}\left(D\right)=\int_{-2}^{1}f\left(t\right)\mathrm{d}t\).
Exemple : Exemple d'une fonction constante
Le plan est rapporté à un repère orthonormal \(\left(O;\vec{\imath} , \vec{\jmath}\right)\).
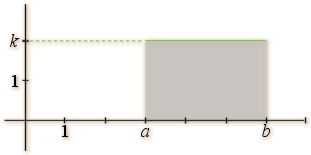
On considère \(A=\displaystyle \int_{a}^{b}k\mathrm{d}x\) avec \(k\geqslant 0\) et \(a\leqslant b\)
Soit \(D\) la partie du plan délimitée par la courbe représentative de la fonction constante \( f : x\mapsto k\), l'axe des abscisses et les droites d'équation \(x = a\) et \(x = b\). La fonction \(f\) est continue positive sur \([a;b]\). L'aire \(A\) en unités d'aire de \(D\) est l'aire d'un rectangle soit : \(A = k(b - a)\).
Exemple :
\(B=\displaystyle \int_{-1}^{1} \sqrt{1-x^{2}}\mathrm{d}x\)
Soit \(D\) la partie du plan délimitée par la courbe de la fonction \( f : x\mapsto \sqrt{1-x^{2}}\), l'axe des abscisses et les droites d'équation \(x = -1\) et \(x = 1\).
La fonction \(f\) est continue positive sur \([-1;1]\).
\( M\left(x;y\right)\in C_{f}\Longleftrightarrow \left\{\begin{array}{l} x\in\left[-1;1\right] \\ y = \sqrt{1-x^{2}} \end{array}\right. \Longleftrightarrow \left\{\begin{array}{l} y\in[0;1]\\ x^{2}+y^{2}=1 \end{array}\right. \)
On remarque que \(C_f\) est le demi-cercle supérieur de centre \(O\) et de rayon \(1\). L'aire \(B\) en unités d'aire de \(D\) est l'aire du demi-disque supérieur de centre \(O\) et de rayon \(1\), soit : \(B=\dfrac12\left(\pi R^{2}\right)=\dfrac{\pi}{2}\).
