Relation de Chasles
Soit \(f\) une fonction définie continue sur un intervalle \(I\) :
Théorème : Chasles
Pour tous réels \(a\), \(b\) et \(c\) de \(I\), \(\displaystyle \int_{a}^{b}f\left(t\right)\mathrm{d}t+ \displaystyle \int_{b}^{c}f\left(t\right)\mathrm{d}t= \displaystyle\int_{a}^{c}f\left(t\right)\mathrm{d}t\).
Exemple :
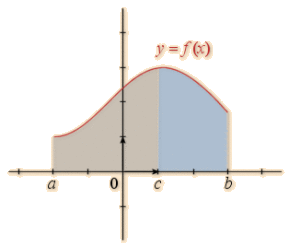
Si \(f\) est une fonction positive et si \(a\leqslant c\leqslant b\), l'aire en unités d'aire de la surface coloriée est égale à la somme des aires en unités d'aire des surfaces grisée et bleutée.
Conséquences
Pour tout réel \(a\) de \(I\), \(\displaystyle \int_{a}^{a}f\left(t\right)\mathrm{d}t=0\).
Pour tous réels \(a\) et \(b\) de \(I\), \(\displaystyle \int_{b}^{a}f\left(t\right)\mathrm{d}t=-\int_{a}^{b}f\left(t\right)\mathrm{d}t\).