Exercice 5
En fin de matinée, un pompiste présente deux listes de valeurs regroupées dans le tableau suivant :
\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline \textrm{PRIX (en euros)} & 39,0 & 52,0 & 19,5 & 65,0 & 32,5 & 58,5 & 26,0 & 45,5 & 71,5\\\hline \textrm{VOLUME (en litres)} & 30 & 40 & 15 & 50 & 25 & 45 & 20 & 35 & 55\\\hline \end{array} \)
Question
Sont-elles proportionnelles ? Si oui, préciser le coefficient de proportionnalité.
Solution
Si elles le sont, le coefficient de proportionnalité est \(\cfrac{30}{39} = \cfrac{10}{13}.\) De plus, on peut remarquer :
\[\begin{array}{lcl}30 = 2 × 15 \text{ et } 39, 0 = 2 × 19, 5&\text{ ; }&45 = 3 × 15 \text{ et } 58, 5 = 3 × 19, 5.\\40 = \cfrac{4} {3} × 30 \text{ et } 52 = \cfrac{4} {3} × 39, 0&\text{ ; }&20 = \cfrac{40}{ 2} \text{ et } 26, 0 = \cfrac{52, 0}{ 2}.\\35 = 20 + 15 \text{ et } 45, 5 = 26, 0 + 19, 5&\text{ ; }&55 = 20 + 35 \text{ et } 71, 5 = 26, 0 + 45, 5.\\50 = 15 + 35 \text{ et } 65, 0 = 19, 5 + 45, 5&\text{ ; }&25 = \cfrac{50} {2} \text{ et } 32, 5 = \cfrac{65, 0} {2}.\end{array}\]
Pour tout prix \(a\) et tout volume \(b\) on a \(\cfrac{a}{b} = \cfrac{10}{13}\). On en déduit que les listes sont proportionnelles.
Question
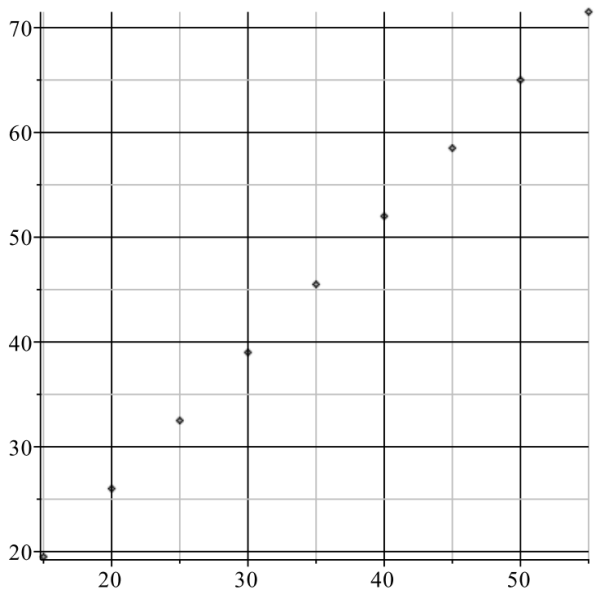
Tracer dans un repère, le graphique qui correspond à ce tableau.
Solution
Le graphique, représentant des points alignés, est le suivant :