Recherche du nombre de solutions d'une équation à l'aide de l'analyse
Le but de l'exercice est de déterminer, suivant les valeurs du paramètre \(m\) réel, le nombre de solutions de l'équation \(x^3 - x^2 + m = 0 (E)\) et d'utiliser les conclusions trouvées pour établir le sens de variation d'une fonction donnée.
Question
Résoudre (\(E\)) dans le cas particulier où \(m = 0\).
Solution détaillée
Pour \(m = 0\), l'équation (\(E\)) devient \(x^3 - x^2 = 0\).
\(x^{3}-x^{2}=0\Longleftrightarrow x^{2}\left(x-1\right)=0\)
L'équation (\(E\)) admet donc 2 solutions dont l'une est double : \(S_{\mathrm{R}}=\{0;1\}\).
Question
Pour \(m\neq0\), on considère la fonction polynôme \(f\) définie sur \(\mathbb R\) par\( f(x) = x^3 - x^2 + m\).
Après avoir étudié les limites de \(f\) en \(+\infty\) et \(-\infty\) et le sens de variation de \(f\), établir le tableau de variation de \(f\).
Solution détaillée
La fonction \(f\) est une fonction polynôme d'où :
\(\begin{array}{l} \displaystyle \lim_{x\rightarrow+\infty}f\left(x\right)=\lim_{x\rightarrow+\infty}x^{3}=+\infty \\ \displaystyle \lim_{x\rightarrow-\infty}f\left(x\right)=\lim_{x\rightarrow-\infty}x^{3}=-\infty \end{array}\)
La fonction \(f\) est une fonction polynôme donc continue et dérivable sur \(\mathbb R\) et pour tout \(x\in \mathbb R, \,\, \)\(f'(x) = 3x^2 - 2x = x(3x - 2)\)
L'expression de \(f'(x)\) est un polynôme du second degré ayant pour racines \(0\) et \(\displaystyle \frac{2}{3}\) donc \(f'(x)\) est positif sur\(\displaystyle\left]-\infty;0\right]\cup\displaystyle \left[\frac{2}{3};+\infty\right[\) (signe de \( a = 3\)) et \(f'(x)\) est négatif sur \(\left[0;\displaystyle \frac{2}{3}\right]\) (signe de \(- a\) )
La fonction \(f\) est donc croissante sur \(]-\infty\,;\,0]\) et sur et \(f\) est décroissante sur \(\left[0;\displaystyle \frac{2}{3}\right]\).

On a \(f(0) = m\) et \(f\left(\displaystyle \frac{2}{3}\right)=m-\dfrac{4}{27}\)
Question
Justifier que sur \( \mathbb R\) , quel que soit le nombre réel \(m\), l'équation \( x^3 - x^2 + m = 0\) admet au moins une solution.
Aide méthodologique
Sait-on de façon générale résoudre par l'algèbre une équation de degré 3 ?
Résoudre l'équation (\(E\)) est équivalent à résoudre sur \(\mathbb R\) l'équation \(f(x) = 0\).
Aide simple
On s'intéresse seulement à l'existence de solutions ; quel théorème permet de justifier l'existence de solutions pour une équation du type \(f(x) = k\) (\(k\) réel) ?
Rappel de cours
D'après le cours, le théorème des valeurs intermédiaires permet de justifier l'existence de solutions dans un intervalle \(I\) pour une équation du type \(f(x) = 0\).
Solution détaillée
D'après l'étude de la fonction \(f\) faite à la question 2 et le tableau de variation trouvé, en appliquant le théorème des valeurs intermédiaires :
Si \(m\geqslant 0\), \(0\in\left]-\infty\,;\,m\right]\) et l'équation \(f(x) = 0\) a une solution dans \(]-\infty;0]\).
Si \(m<0\), \(0\displaystyle \in\left[m-\frac{4}{27}\,;\,+\infty\right[\) car et l'équation \( f(x) = 0\) admet une solution dans \(\left[\displaystyle \frac{2}{3}\,;\,+\infty\right[\).
Pour tout \(m\), l'équation \((E)\) admet donc au moins une solution dans \(\mathbb R\) .
Question
Pour quelles valeurs du nombre réel \(m\) l'équation \(x^3 - x^2 + m = 0\) admet-elle :
3 solutions (distinctes ou non) ?
une seule solution ?
Rappel de cours
D'après le cours, pour justifier l'existence et l'unicité d'une solution pour une équation du type \(f(x) = 0\) dans un intervalle \(I\), il faut démontrer que \(f\) est continue et strictement monotone sur \(I\) et que \(0\in f\left(I\right)\) ; \(f(I)\) désignant l'intervalle image de \(I\). L'étude du tableau de variation de \(f\) permet de vérifier les conditions exigées.
Solution détaillée
Rappel : Tableau de variation de f

D'après l'étude de \(f\), \(f\) est continue et strictement monotone sur chacun des intervalles \(I_1 = ]-\infty;0]\), \(I_{2}=\left[0;\displaystyle \frac{2}{3}\right]\) et \(I_{3}=\left[\displaystyle \frac{2}{3};+\infty\right[\) d'où :
Pour \(0\leqslant m\leqslant\frac{4}{27}\), l'étude du tableau de variation montre l'existence d'une solution unique sur chacun des intervalles \( I_1, I_2, I_3\) donc de 3 solutions pour l'équation \(f(x) = 0\).
On peut remarquer les deux cas particuliers :
pour m = \(0,\) \(0\) est racine double,
pour \( m = \dfrac4{27} \), \(\displaystyle \frac{2}{3}\) est racine double.
Pour \(m < 0\), l'étude du tableau de variation montre l'existence d'une seule solution dans \(\left[\displaystyle \frac{2}{3}\,;\,+\infty\right[\).
Pour \( m > \dfrac4{27} \), l'étude du tableau de variation montre l'existence d'une seule solution dans \(]-\infty\,;\,0]\).
Question
Soit \(g\) la fonction définie sur \(\displaystyle \mathbb{R}-\left\{\frac{2}{3}\right\}\) par \(g\left(x\right)=\dfrac{3x^{3}+9x} { 3x - 2} \).
Justifier qu'il existe un nombre réel \(\alpha\) tel que le sens de variation de \(g\) soit :
\(g\) est décroissante sur \(\left]-\displaystyle \infty\,;\,\dfrac{2}{3}\right[\) et sur \(\left]\displaystyle \dfrac{2}{3}\,;\,\alpha \right]\),
\(g\) est croissante sur \([\alpha\,;\,+\infty[\).
Aide méthodologique
Le sens de variation de \(g\) peut s'obtenir à l'aide du signe de \(g'\) fonction dérivée de \(g\).
Aide simple
L'étude précédente de l'équation \(x^3 - x^2 + m\) pour m quelconque peut être utile.
Solution détaillée
La fonction \(g\) est une fonction rationnelle donc dérivable sur son ensemble de définition et pour tout \(x\displaystyle \in \mathbb{R}-\left\{\frac{2}{3}\right\}\),
\( \begin{array}{rcl} g'\left(x\right)&=& \dfrac{\left(9x^{2}+9\right)\left(3x-2\right)-3\left(3x^{3}+9x\right)}{\left(3x-2\right)^{2}} \\ &=&\dfrac{18\left(x^{3}-x^{2}-1\right)}{\left(3x-2\right)^{2}} \end{array} \)
Pour tout \(x\displaystyle \in \mathbb{R}-\left\{\dfrac{2}{3}\right\}\), \((3x - 2)^2 > 0\) et \(g'(x)\) est donc du signe du polynôme \(x^3 - x^2 - 1\).
L'étude précédente de la fonction \(f\) pour \(m = -1\) (cas \(m < 0\)) justifie l'existence et l'unicité d'un réel \(\displaystyle \alpha\in\left]\frac{2}{3}\,;\,+\infty\right[\) solution de l'équation \(x^3 - x^2 - 1 = 0\) et l'on a :
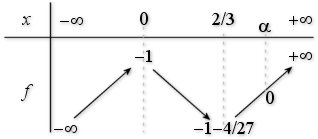
L'étude du tableau de variation de la fonction\(f\) pour \(m = - 1\) permet de conclure que :
sur \(\left]-\displaystyle \infty\,;\,\dfrac{2}{3}\right[ \cup \displaystyle \left ] \dfrac{2}{3}\,;\,\alpha \right ]\), \(g'\left(x\right)\leqslant 0\),
sur \([\alpha\,;\,+\infty[\), \(g'\left(x\right)\geqslant 0\).
On peut donc conclure qu'il existe un réel \(\alpha\) tel que \(g\) est décroissante sur \(\left]-\displaystyle \infty\,;\,\dfrac{2}{3}\right[\) et sur \(\left]\displaystyle \dfrac{2}{3}\,;\,\alpha\right]\), \(g\) est croissante sur l'intervalle l'intervalle \([\alpha\,;\,+\infty[\).
Question
Déterminer les limites de la fonction \(g\) en \(+\infty\), \(-\infty\) et \(\displaystyle \frac{2}{3}\).
Solution détaillée
La fonction \(g\) est une fonction rationnelle d'où :
\(\begin{array}{l} \displaystyle \lim_{x\rightarrow+\infty}g\left(x\right)=\lim_{x\rightarrow+\infty}\frac{3x^{3}}{3x}=\lim_{x\rightarrow+\infty}x^{2}=+\infty \\ \displaystyle \lim_{x\rightarrow-\infty}g\left(x\right)=\lim_{x\rightarrow\infty}\frac{3x^{3}}{3x}=\lim_{x\rightarrow-\infty}x^{2}=+\infty \end{array} \)
\( \left.\begin{array}{l} \displaystyle \lim_{x\rightarrow \frac{2}{3}} 3x^{3}+9x=\frac{62}{9}\\ \displaystyle \lim_{x\rightarrow \dfrac{2}{3}}3x-2=0 \end{array}\right\}\) d'où \(\displaystyle \lim_{\substack{x\rightarrow\frac23 \\ x>\frac23}}g\left(x\right) = +\infty \) et \(\displaystyle\lim_{\substack{x\rightarrow\frac23 \\ x<\frac23}}g\left(x\right) = -\infty\).
Remarque :
On se souvient que : si \(x>\frac23\) alors, \(x-\displaystyle \frac{2}{3}>0\) et si \(x<\displaystyle \dfrac{2}{3}\) alors, \(x-\displaystyle \frac{2}{3}<0\).
Question
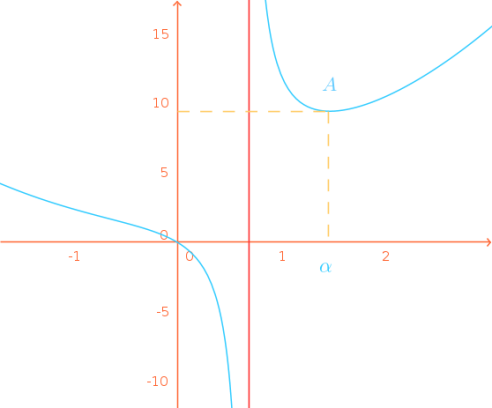
Après avoir justifié que \(1,47\) est une valeur approchée de \(\alpha\) par excès à \(10^{-1}\) près, et en prenant \(1,47\) pour \(\alpha\), construire la représentation graphique de \(g\) dans un repère orthogonal \(\left(O,\vec{\imath}, \vec{\jmath} \right)\).
Aide méthodologique
Le nombre réel \(b\) est une valeur approchée de \(\alpha\) par excès à \(10^{-1}\) près s'il vérifie \(b-0,1\leqslant\alpha\leqslant b\).
Solution détaillée
A l'aide de la machine à calculer, on sait que \(g(1,46) < 0 \mbox { et } g(1,47) > 0\) donc que \(g(1,46) < g (\alpha)< g(1,47)\) ; d'après l'étude de la fonction \(g\), \(g\) est croissante sur \(\left[\displaystyle \frac{2}{3};+\infty\right[\) d'où \(1,46\leqslant\alpha\leqslant 1,47\) et \(1,47\) est bien une valeur approchée par excès de \(\alpha\) à \(10^{-1}\) près.
Représentation graphique de g
Les résultats sur les limites de \(g\) en \(\frac23\) permettent de savoir que la droite d'équation \(x=\frac23\) est asymptote à la représentation graphique de \(g\).
x | -1 | 0 | 1 | 1,47 | 2 |
g(x) | 2,4 | 0 | 12 | 9,4 | 10,5 |