Etude d'une fonction à l'aide de la représentation graphique de sa dérivée
Soit une fonction \(f\) définie et dérivable sur \([-2\,;\,2]\).
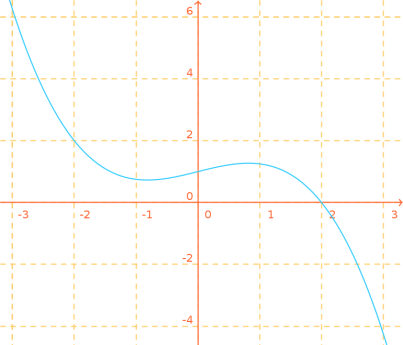
La courbe représentative de la fonction \(f'\) est donnée ci-dessous :
Question
Démontrer que la fonction \(f\) est monotone sur \([-2\, ;\,2]\).
Aide méthodologique
La fonction \(f\) est monotone sur \([-2\, ;\, 2]\) si elle garde un signe constant sur \([-2\, ;\,2]\).
Solution détaillée
Sur l'intervalle \([-2 \,;\,2]\), la fonction \(f'\) est strictement positive sauf en 2 car \(f'(2) = 0\).
Donc la fonction \(f\) est strictement croissante sur \([-2 \,;\,2]\).
Et donc la fonction \(f\) est bien monotone sur l'intervalle \([-2 \,;\,2]\).
Question
La fonction \(f\) admet-elle un extremum en \(0\) ?
Aide simple
Si la fonction \(f\) admet un extremum en \(x=a\) alors, \(f'(a) = 0\).
Aide détaillée
Réciproquement : si la fonction \(f'\) s'annule en changeant de signe en \(x = a\) alors, la fonction \(f\) admet un extremum en \(x = a\).
Solution simple
On a \(f'(0) = 1\). Donc la fonction \(f\) n'admet pas d'extremum en \(0\).
Question
Au point d'abscisse \(x = 0\), la courbe représentative de la fonction \(f\) admet-elle une tangente parallèle à la droite d'équation \(y=x\)?
Aide simple
Quel est le coefficient directeur de la tangente au point d'abscisse \(x=0\) ?
Solution détaillée
Par définition le coefficient directeur de la tangente au point d'abscisse \(x=0\) est égal à :\(f'(0) = 1\). Or le coefficient directeur de la droite d'équation \(y = x\) est \(1\).
Deux droites parallèles ayant le même coefficient directeur, la courbe représentative de la fonction \(f\) admet au point d'abscisse \(x = 0\) une tangente parallèle à la droite d'équation \(y = x\).
Question
Peut-on affirmer que pour tout \(x\) de \([-2;2]\), \(f\left(x\right)\geqslant 0\)?
Rappel de cours
Utilisez le corollaire du théorème des valeurs intermédiaires
Corollaire |
|---|
Soit \(f\) une fonction définie, continue et strictement monotone sur un intervalle \([a;b]\). Pour tout réel \(k\) compris entre \(f(a)\) et \(f(b)\), il existe un et un seul réel \(c\) dans l'intervalle \([a\,;\,b]\) tel que \(f(c) = k\) (c'est-à-dire : l'équation \(f(x) = k\) a une solution unique dans l'intervalle \([a\,;\,b]\)). |
Solution détaillée
D'après la question 1), \(f\) est strictement croissante sur \([-2;2]\).
Donc pour tout nombre réel \(x\) de \([-2\,;\, 2]\), \(f\left(x\right)\geqslant f\left(-2\right)\).
Si \(f\left(-2\right)\geqslant 0\), alors pour tout réel \(x\) de\( [-2\,;\,2]\),\(f\left(x\right)\geqslant 0\), et l'affirmation est vraie.
Par contre si \(f\left(-2\right)<0\), alors on utilise le théorème des valeurs intermédiaires.
Comme la fonction \(f\) est continue (car dérivable) sur \([-2;2]\) et strictement croissante sur \([-2;2]\), on choisit \(k\) tel que \(f(-2) < k < 0\) et \(k < f(2)\) ; l'équation \(f(x) = k\) admet une solution unique dans l'intervalle \( [-2\,;\,2] \) et dans ce cas \(f(x) = k < 0\) et l'affirmation est fausse.
Bilan |
|---|
L'affirmation est vraie lorsque \(f\left(-2\right)\geqslant 0\) et fausse sinon. |
Question
L'équation \(f(x) = 0\) admet-elle plus de deux solutions ?
Aide simple
Attention, ne pas confondre les équations \( f(x) = 0\) et \(f'(x) = 0\) .
Rappel de cours
Penser au théorème des valeurs intermédiaires.
Solution détaillée
Comme la fonction \(f\) est continue (car dérivable) sur \([-2\,;\,2]\) et strictement croissante sur \([-2\,;\,2]\), on utilise le théorème des valeurs intermédiaires.
Si \(f(-2) < 0 < f(2)\), alors l'équation \(f(x) = 0\) admet une unique solution.
Si \(f(-2) < f(2) < 0\), alors l'équation \(f(x) = 0\) n'admet pas de solution.
Si \(f(-2) = 0\), ou si \( f(2) = 0\) alors l'équation \(f(x) = 0\) admet une unique solution.
Si \(f(-2) > 0\), alors comme \(f\) est strictement croissante, on a : pour tout réel \(x\) de \([-2;2]\), \(f\left(x\right)\geqslant f\left(-2\right)>0\) et \(f\) ne s'annule pas sur \([-2;2]\).
En conclusion : |
|---|
Si la fonction \(f\) s'annule alors elle ne s'annule qu'en au plus une valeur. Donc l'équation \(f(x) = 0\) n'admet pas plus de deux solutions mais au plus une ( une ou zéro) |