Etude globale d'une fonction rationnelle
Soit la fonction \(f\) définie par \(f\left(x\right)=\displaystyle \frac{4x+b}{2x^{2}+bx+c}\).
Question
Déterminer les nombres réels \(b\) et \(c\) pour que la fonction \(f\) admette deux extrema en \(x = -2\) et \(x = 1\).
Aide méthodologique
Si la fonction\(f\) admet un extremum en \(x = a\) alors \(f'(a) = 0\).
Aide simple
Réciproquement : si la fonction \(f\)' s'annule en changeant de signe en \(x = a\) alors la fonction \(f\) admet un extremum en \(x = a\) .
Aide détaillée
Le calcul de \(f'(x)\) permet de conclure que \(f'(x)\) a le même signe que \(-8x^2 -4xb +(4c-b^2)\).
Solution détaillée
On calcule \(f'\left(x\right)=\displaystyle \frac{-8x^{2}-4xb+\left(4c-b^{2}\right)}{\left(2x^{2}+bx+c\right)^{2}}\).
Nécessairement \(f'(-2) = 0 \mbox{ et } f'(1) = 0\) ; or \(f'\left(-2\right)=\displaystyle \frac{-32+8b+\left(4c-b^{2}\right)}{\left(8-2b+c\right)^{2}}\) et \(f'\left(1\right)=\displaystyle \frac{-8-4b+\left(4c-b^{2}\right)}{\left(2+b+c\right)^{2}}\).
\(\left\{\begin{array}{rcl} f'\left(-2\right)&=&0 \\ f'\left(1\right)&=&0 \end{array}\right. \Longleftrightarrow \left\{\begin{array}{rcl} -32+8b+\left(4c-b^{2}\right)&=&0\\ -8-4b+\left(4c-b^{2}\right)&=&0 \end{array}\right. \)
En soustrayant membre à membre, on obtient \(b = 2\) puis \(c = 5\).
Attention :
Cette condition est nécessaire mais non suffisante. Il est donc indispensable de vérifier que pour \(b = 2\) et \(c = 5\), \(f'(x)\) s'annule en changeant de signe pour \(x = -2\) et \(x = 1\).
Or \(f'\left(x\right)=\displaystyle \frac{-8x^{2}-8x+16}{\left(2x^{2}+2x+5\right)^{2}}=\frac{-8\left(x-1\right)\left(x+2\right)}{\left(2x^{2}+2x+5\right)^{2}}\)et \(f'(x)\) s'annule en changeant de signe pour \(x = -2\) et \(x = 1\).
Question
On pose \(g\left(x\right)=\displaystyle \frac{4x+2}{2x^{2}+2x+5}\).
Déterminer l'ensemble de définition de la fonction \(g\).
Étudier les limites de la fonction \(g\) aux bornes de son ensemble de définition (on pourra en déduire l'existence d'asymptotes à \(C_g\)).
Après avoir précisé l'ensemble de dérivabilité de la fonction \(g\), déterminer \(g'(x)\).
Étudier les variations de la fonction \(g\) puis dresser le tableau de variations de \(g\).
Aide méthodologique
Une fonction rationnelle (quotient de deux polynômes) a les mêmes limites en \(-\infty\) et en \(+\infty\) que le quotient des termes de plus haut degré.
Une fonction rationnelle est dérivable sur son ensemble de définition.
On pourra réutiliser les résultats de la toute première question de l'exercice.
Solution détaillée
Le trinôme du second degré \(2x^2 + 2x + 5\) ne s'annule pas car \(\Delta=-16<0\) ; par conséquent \(g\) est définie sur \( \mathbb R\).
Une fonction rationnelle (quotient de deux polynômes) a les mêmes limites en \(-\infty\) et en \(+\infty\) que le quotient des termes de plus haut degré.
\(\displaystyle \lim_{x\rightarrow\pm{\infty}}g\left(x\right)=\lim_{x\rightarrow\pm\infty}\frac{4x}{2x^{2}}=\lim_{x\rightarrow\pm{\infty}}\frac{2}{x}=0\)
On en déduit que l'axe des abscisses est asymptote à \(C_g\) en \(-\infty\) et en \(+\infty\) .
La fonction \(g\) est une fonction rationnelle dérivable sur son ensemble de définition \(\mathbb R\).
\(\begin{array}{rcl}g'\left(x\right)&=&\dfrac{4\left(2x^{2}+2x+5\right)-\left(4x+2\right)\left(4x+2\right)}{\left(2x^{2}+2x+5\right)^{2}} \\&=&{\dfrac{-8\left(x^{2}+x-2\right)}{\left(2x^{2}+2x+5\right)^{2}}}\\&=&{\dfrac{-8\left(x-1\right)\left(x+2\right)}{\left(2x^{2}+2x+5\right)^{2}}}\end{array}\)
Comme \((2x^2 + 2x +5)^2 > 0\) ; le signe de\( g'(x)\) ne dépend que de celui de \(-8(x - 1)(x+2)\).
Remarque :
On peut remarquer que \(g\) est la fonction déterminée dans la toute première question de l'exercice avec \(b = 2\) et \(c = 5\). Donc on retrouve le fait que \(g'(x)\) s'annule en changeant de signe en \(x = -2\) et \(x = 1\).
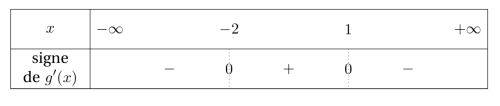
D'où l'étude des variations de la fonction \(g\) :

Question
On pose \(g\left(x\right)=\displaystyle \frac{4x+2}{2x^{2}+2x+5}\).
Donner une équation de la tangente \(T\) à \(C_g\) au point \(A\) de corrdonnées \((-\dfrac 12\, ; \, 0).\)
Solution détaillée
Une équation de la tangente \(T\) à \(C_g\) au point d'abscisse \(a\) est : \(y = g'(a)(x-a) + g(a)\).
Comme \(g \left( -\dfrac{1}{2} \right) =0\) et \(g' \left(-\dfrac12\right) =\displaystyle \dfrac{8}{9}\), une équation de \(T\) est : \(y=\displaystyle \dfrac{8}{9}\left(x+\dfrac{1}{2}\right)\).
Question
On pose \(g\left(x\right)=\displaystyle \frac{4x+2}{2x^{2}+2x+5}\).
Étudier la position de \( C_g\) par rapport à \(T\).
Aide méthodologique
Étudier la position de \( C_g\) par rapport à une droite \(D\) d'équation \(y = ax + b\) revient à étudier le signe de \(g(x) - y\).
Si \(\left\{\begin{array}{l} f\left(x\right)-\left(ax+b\right)>0,\mathrm{ \mbox {alors} \ C_g \ \mbox{ est au-dessus de } D}\\ f\left(x\right)-\left(ax+b\right)<0,\mathrm{ \mbox{ alors } \ C_g \ \mbox{ est en-dessous de } D}\\ \end{array}\right.\).
Solution détaillée
Étudier la position de \( C_g\) par rapport à la droite \(T\) d'équation \(y=\displaystyle \frac{8}{9}\left(x+\frac{1}{2}\right)\) revient à étudier le signe de \(g(x) - y\).
\(g\left(x\right)-y=\displaystyle \frac{4x+2}{\left(2x^{2}+2x+5\right)}-\frac{8}{9}\left(x+\frac{1}{2}\right)\)
\(g\left(x\right)-y=\displaystyle \frac{2\left(2x+1\right)}{\left(2x^{2}+2x+5\right)}-\frac{4}{9}\left(2x+1\right)\)
\(g\left(x\right)-y=\displaystyle \frac{2\left(2x+1\right)}{9\left(2x^{2}+2x+5\right)}\left(9-2\left(2x^{2}+2x+5\right)\right) \)
\(g\left(x\right)-y=\displaystyle \frac{2\left(2x+1\right)}{9\left(2x^{2}+2x+5\right)}\left(-4x^{2}-4x-1\right)\)
\(g\left(x\right)-y=\displaystyle \frac{-2\left(2x+1\right)}{9\left(2x^{2}+2x+5\right)}\left(2x+1\right)^{2}\)
\(g\left(x\right)-y=\displaystyle \frac{-2\left(2x+1\right)^{3}}{9\left(2x^{2}+2x+5\right)}\)
Le signe \(g(x) - y\) ne dépend que de celui de \(2x+1\). Donc :
Sur \(\left]-\displaystyle \infty\,;\,-\frac{1}{2}\right[\); \(g\left(x\right)-y>0\Longleftrightarrow g\left(x\right)>y\). La courbe \( C_g\) est au-dessus de \(T\).
Sur \(\left]-\displaystyle \frac{1}{2}\,;\,+\infty\right[\); \(g\left(x\right)-y<0\Longleftrightarrow g\left(x\right)<y\). La courbe \( C_g\) est en-dessous de \(T\).
Question
On pose \(g\left(x\right)=\displaystyle \frac{4x+2}{2x^{2}+2x+5}\).
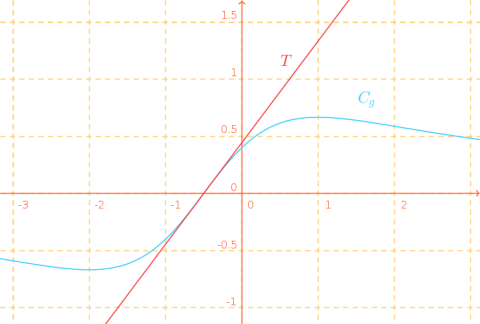
Tracer \(T\) et \( C_g\) dans un repère orthonormal \(\left(O;\vec{\imath} , \vec{\jmath} \right)\).
Solution simple
Représentation de \( C_g\) et de sa tangente \(T\) sur l'intervalle \([-3\, ; \, 3]\).