Exercice de recherche : Étude d'une fonction non déterminée par son expression
Soit \(f\) est une fonction deux fois dérivable sur \(\mathbb R\). C'est-à-dire que la fonction \(f\) est dérivable et que sa fonction dérivée \(f'\) est elle même dérivable. On note \(f"\) la dérivée de la fonction \(f'\).
\(C_f\) désigne sa représentation graphique dans le plan rapporté à un repère orthonormal \( \left( O ; \vec{\imath},\vec{\jmath} \right) \).
On donne les informations suivantes :
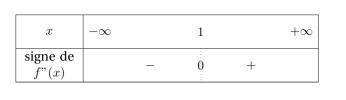
Le tableau de signe de la fonction \(f''\) est le celui ci-contre.
On sait également que \( f'\left(x\right)=0\Longleftrightarrow x=0\) ou \(x = 4\) ; \(f'(1) = - 3\),
que \(f\left(x\right)=0\Longleftrightarrow x=-1\) ou \(x = 1\) ou \(x = 7\) ; \(f(0) = 1\) ; \(f(4) = - 2\),
et que \(\displaystyle \lim_{x\rightarrow-{\infty}}\left(f\left(x\right)-\frac32x-3\right)=0\) ; \(\displaystyle \lim_{x\rightarrow+\infty}\left(f\left(x\right)-2x+16\right)=0 \).
Question
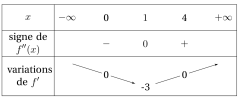
Dresser le tableau de variations de la fonction \(f'\).
Justifier les limites de la fonction \(f\) en \(-\infty\) et en \(+\infty\).
Dresser le tableau de variations de la fonction \(f\).
Aide méthodologique
L'étude du signe de la fonction dérivée d'une fonction permet d'étudier les variations de cette fonction. Penser à prendre en compte toutes les données de l'exercice.
Solution détaillée
On dresse le tableau de variations de la fonction \(f'\) :
Par ailleurs, d'après les hypothèses
\(\displaystyle \lim_{x\rightarrow-{\infty}}f\left(x\right)=\lim_{x\rightarrow-{\infty}}\left(\dfrac{3}{2}x+3\right)=-\infty\), et
\(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=\lim_{x\rightarrow+\infty}\left(2x-16\right)=+\infty \).
Nota bene : |
|---|
les droites \(D_1\) d'équation \( y = \frac32x + 3 \) et \(D_2\) d'équation \(y = 2x - 16 \) sont respectivement asymptotes à \(C_f\) en \(-\infty\) et en \(+\infty\). |
Puis on en déduit le signe de la fonction \(f'\) et le tableau de variations de \(f\).
Question
Déterminer une équation de la droite \(T\) tangente à \(C_f\) au point d'abscisse 1.
Aide méthodologique
Revoir l'équation générale de la tangente à \(C_f\) au point d'abscisse \(a\).
Aide détaillée
Une équation de la tangente à \(C_f\) au point d'abscisse \(a\) est : \(y=f'\left(a\right)\left(x-a\right)+f\left(a\right)\).
Solution détaillée
Une équation de la tangente à \(C_f\) au point d'abscisse \(a\) est :
\(y = f'(a) (x-a) + f(a)\)
En appliquant avec \(a=1\) ; on obtient \(f(1) = 0\) et \(f'(1) = -3\).
D'où une équation de la tangente \(T\) : \(y = -3x + 3\)
Question
Tracer \(C_f\) en tenant compte des informations données et des résultats des questions précédentes.
Aide à la lecture
Relire soigneusement toutes les informations ; ne pas oublier :
l'interprétation géométrique du nombre dérivée \(f'(x)\),
la définition des asymptotes à une courbe.
Solution détaillée
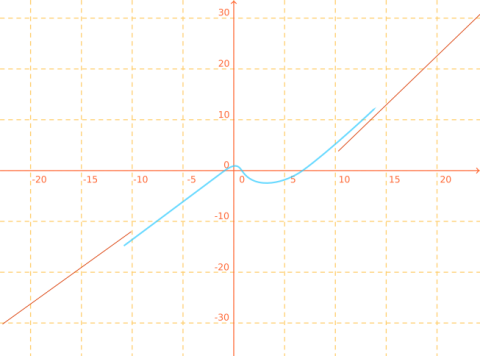
On place les points de coordonnées \((-1\, ; \,0)\) ; \((0 \,;\,1)\) ; (\(1\, ;\, 0)\) ; \((4\,; \,-2)\) ; \((7\, ;\,0).\)
On trace les tangentes horizontales en les points \((0\, ;\,1)\) et \((4\, ;\, -2)\).
On trace la tangente \(T\) et les deux asymptotes \(D_1\) et \(D_2\).
On obtient un graphique du type :
