Exemples d'étude d'une courbe de fonction rationnelle
On définit la fonction \(f\) par : \(f\left(x\right)=\displaystyle \frac{2x^{2}+x-13}{x^{2}-x-2}\).
\((C)\) est sa représentation graphique dans le repère \(\left(O;\vec \imath,\vec \jmath \right)\).
Question
Etudier les variations de \(f\) sur son ensemble de définition \(D_f\).
Aide méthodologique
Il s'agit d'une étude classique de fonction ; reprendre le plan d'étude générale : étudier les limites de \(f\) aux bornes de son ensemble de définition, calculer sa dérivée, puis étudier les variations de \(f\).
Aide détaillée
Règles opératoires :
La limite en \(+\infty\) ou \(-\infty\) d'une fonction rationnelle est égale à la limite du quotient des termes de plus haut degré de son numérateur et de son dénominateur :
Dérivée d'un quotient :
Soient \(u\) et \(v\) deux fonctions dérivables sur un intervalle \(I\) alors la fonction \(\dfrac{u}{v}\) est dérivable en tout point de son ensemble de définition et on a :
\(\left(\displaystyle \frac{u}{v}\right)'=\dfrac{u'\times v-v'\times u}{v^{2}}\)
Solution détaillée
Le trinôme \(x^2 - x - 2\) admet deux racines : -1 et 2.
Donc \(f\) est définie sur \(D_{f}=\mathbb{R}-\{-1;2\}\).
Étude des limites de la fonction \(f\) en \(\pm\infty\)
La limite en \(+\infty\) ou \(-\infty\) d'une fonction rationnelle est égale à la limite du quotient des termes de plus haut degré de son numérateur et de son dénominateur
\(\displaystyle \lim_{x\rightarrow\pm{\infty}}f\left(x\right)=\lim_{x\rightarrow\pm{\infty}}\frac{2x^{2}+x-13}{x^{2}-x-2}=\lim_{x\rightarrow\pm{\infty}}\dfrac{2x^{2}}{x^{2}}=2\)
Étude de la limite de la fonction \(f\) en \(-1 \, : \)
\(\displaystyle \lim_{x \to -1}\left(2x^{2}+x-13\right)=-12\) et \(\displaystyle \lim_{x \to -1}\left(x^{2}-x-2\right)=0\).
D'après le signe du trinôme on étudie les limites à droite et à gauche de \(-1\) :
1er cas : \(\displaystyle \lim_{\substack{x\rightarrow-1 \\ x<-1}}\left(x^{2}-x-2\right)=0 \) et \(x^2 - x - 2 > 0\) , donc \(\displaystyle \lim_{\substack{x\rightarrow-1 \\ x<-1}} f\left(x\right)=-\infty\).
2ème cas : \(\displaystyle \lim_{\substack{x\rightarrow-1 \\ x>-1}} \left(x^{2}-x-2\right)=0 \) et \(x^2 - x - 2 < 0\) , donc \(\displaystyle \lim_{\substack{x\rightarrow-1 \\ x>-1}} f\left(x\right)=+\infty \).
Étude de la limite de la fonction \(f\) en \(2\) :
\(\displaystyle \lim_{x \to 2}\left(2x^{2}+x-13\right)=-3\) et \(\displaystyle \lim_{x \to 2}\left(x^{2}-x-2\right)=0\).
D'après le signe du trinôme on étudie les limites à droite et à gauche de \(2\) :
1er cas : \(\displaystyle\lim_{\substack{x \to 2\\ x<2}}\left(x^{2}-x-2\right)=0\) et \(x^2 - x - 2 < 0\), donc \(\displaystyle \lim_{\substack{x\rightarrow 2 \\ x<2}} f\left(x\right)=+{\infty} \).
2ème cas : \(\displaystyle \lim_{\substack{x\rightarrow 2 \\ x>2}}\left(x^{2}-x-2\right)=0\) et \(x^2 - x - 2 > 0\), donc \(\displaystyle \lim_{\substack{x\rightarrow 2 \\ x>2}}f\left(x\right)=-{\infty} \).
Conséquences : on peut en déduire que les droites d'équations respectives : \( y = 2\) ; \(x = -1\) ; \(x = 2\) sont asymptotes à \((C)\).
Calcul de la dérivée de \(f\)
f est une fonction rationnelle dérivable sur son ensemble de définition \(D_{f}\).
\( \begin{array}{rcl} f'\left( x \right) &=& \dfrac{\left(4x+1\right) \left( x^2 - x - 2 \right) - \left( 2x - 1 \right) \left(2x ^2 + x - 13 \right) }{\left( x ^2 - x - 2 \right) ^2 } \\ &=& \dfrac{-3x ^2 + 18x - 15}{\left( x ^2 - x - 2\right) ^2 } = \dfrac{ -3\left( x - 1 \right) \left( x - 5 \right) }{\left( x ^2 - x - 2 \right) ^2} \end{array}\)
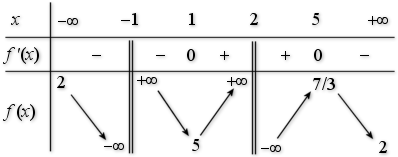
Etude des variations de \(f\)
\((x^2 - x - 2 )^2\) étant strictement positif sur \(D_{f}\) . Le signe \(f'(x)\) de ne dépend que de celui de \(-3(x - 1)(x - 5)\).
Sur \(]-\infty;-1[\), \( ]-1;1[\) et sur \(]5;+\infty[\) , \( f'(x)\) est strictement négatif et \(f\) est strictement décroissante.
Sur \(]1;2[\) et sur \(]2;5[\), \(f'(x)\) est strictement positif et \(f\) est strictement croissante.
Question
Déterminer les réels \(a\) et \(b\) tels que :
pour tout \(x\) de \(D_f\), \(f\left(x\right)=2+\displaystyle \frac{ax+b}{x^{2}-x-2}\).
En déduire les coordonnées du point \(A\) où la courbe coupe son asymptote horizontale.
Aide méthodologique
Penser à utiliser les résultats du calcul de limite de la question 1.
Une simple recherche d'intersection de courbe et de droite permet de conclure.
Solution détaillée
Pour tout \(x\) de \(D_f\), \(2+\displaystyle \frac{ax+b}{x^{2}-x-2}=\frac{2x^{2}+\left(a-2\right)x+b-4}{x^{2}-x-2}\).
Par identification avec la forme de \(f(x)\) on obtient : \(a - 2 = 1\) et \(b - 4 = -13\).
D'où \(a = 3\) et \(b = -9\).
Donc pour tout \(x\) élément de \(D_f\), \(f\left(x\right)=2+\displaystyle \frac{3x-9}{x^{2}-x-2}\).
D'après la question 1, on a \(\displaystyle \lim_{x\rightarrow\pm{\infty}} f\left(x\right)=2\). Donc la droite d'équation \(y = 2\) est asymptote horizontale à \((C)\) en \(\pm\infty\).
\(M(x;y)\) est un point d'intersection de cette asymptote et de \((C)\) si et seulement si \(\left\{\begin{array}{l} y=f\left(x\right),\,\, x\in D_{f} \\ y=2 \end{array}\right. \).
Soit \(x\in{D_f}\), \(f\left(x\right)=2\displaystyle \Longleftrightarrow 2+\frac{3x-9}{x^{2}-x-2}=2\Longleftrightarrow 3x-9=0\Longleftrightarrow x=3\).
Donc \((C)\) coupe son asymptote horizontale en le point \(A(3;2)\).
Question
Donner une équation de la droite \(\Delta\) tangente à \((C)\) au point \(A\).
Déterminer les coordonnées du point \(B\) où cette tangente recoupe \((C)\).
Aide méthodologique
Une équation de la tangente à \(C_f\) au point d'abscisse a est : \(y=f'\left(a\right)\left(x-a\right)+f\left(a\right)\).
Une simple recherche d'intersection de courbe et de droite permet de conclure.
Solution détaillée
Une équation de la tangente à \((C)\) au point d'abscisse \(3\) est :
\(y = f'(3)(x - 3) + f(3)\)
Or \(f'\left( 3 \right) = \frac34 \) et \(f(3) = 2\) d'où l'équation : \(y=\displaystyle \frac{3}{4}\left(x-3\right)+2=\frac{3}{4}x-\frac{1}{4}\).
Le point \(M(x\,;\, y)\) est un point d'intersection de cette tangente et de \((C)\) si et seulement si : \(\left\{\begin{array}{l} y=f\left(x\right),x\in D_{f}\\ y=\dfrac34x-\dfrac14 \end{array}\right.\).
On résout cette équation :
\(f\left(x\right)=\displaystyle \dfrac{3}{4}\left(x-3\right)+2\Longleftrightarrow 2+\dfrac{3x-9}{x^{2}-x-2}=2+\dfrac{3}{4}\left(x-3\right)\Longleftrightarrow\dfrac{3\left(x-3\right)}{x^{2}-x-2}=\dfrac{3\left(x-3\right)}{4}\)
On cherche le point en lequel la courbe \((C)\) recoupe la tangente donc on peut supposer que \(x\neq 3\).
\(x^{2}-x-2=4\Longleftrightarrow x^{2}-x-6=0\Longleftrightarrow\left(x-3\right)\left(x+2\right)=0\)
On retrouve \(x = 3\) ou \(x = -2\).
Donc la courbe\( (C)\) recoupe la tangente \(\Delta\) au point \(B\left(-2\,;\,-\displaystyle \frac{7}{4}\right)\).
Question
Tracer dans le repère \(\left(O;\vec \imath,\vec \jmath \right)\) : \((C)\), \(\Delta\), \(A\) et \(B\).
Solution simple
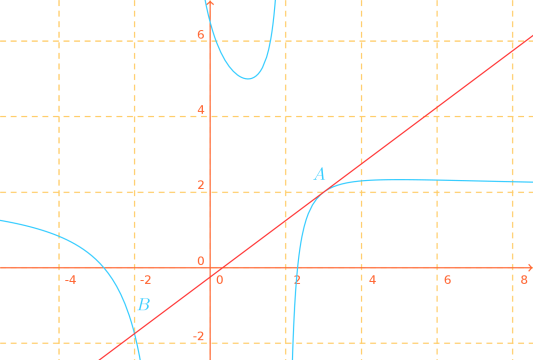
Représentation de la courbe \((C)\), en turquoise, de la droite \(\Delta\), en rouge, et des points \(A\) et \( B\)