Approcher la solution réelle d'une équation
Soit la fonction \(f\) définie et continue sur \(\mathbb R\) par : \(f\left(x\right)=x^{3}+x^{2}+3x-4\).
Question
Donner le tableau de variations de la fonction \(f\).
Justifier que l'équation \(f(x) = 0\) a une solution unique \(\alpha\) dans \(\mathbb R\).
Donner, par encadrements successifs, une valeur approchée de \(\alpha\) à \(10^{-1}\) près.
Solution détaillée
La fonction \(f\) est dérivable sur \(\mathbb R\) et sa dérivée est définie par \(f'(x)=3x^2+2x+3\).
Pour tout nombre réel \(x\), on a \(f'(x) > 0\) (le trinôme du second degré \(3x^2 + 2x +3\) a un discriminant négatif, donc il garde un signe constant).
La fonction \(f\) est donc une fonction strictement croissante sur \(\mathbb R\) de plus elle est continue sur \( \mathbb R\) (puisqu'elle est dérivable).
On obtient les limites de la fonction \(f\) en utilisant les règles opératoires :
\(\displaystyle \lim_{x\to-\infty} f\left(x\right)=\lim_{x\to-\infty} x^{3}=-\infty \) et \(\displaystyle \lim_{x\to+\infty} f\left(x\right)=\lim_{x\to+\infty} x^{3}=+\infty \).
On peut alors donner le tableau de variations de \(f\) :
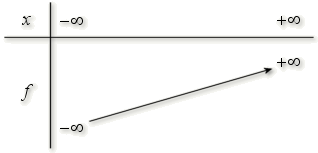
D'après les résultats précédent sur la fonction \(f\), l'équation \(f(x) = 0\) a une solution unique dans \( \mathbb R\) :
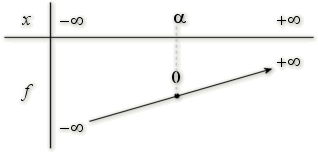
On peut remarquer que \(f(0) = -4\) et \(f(1) = 1\).
Le nombre réel \(f(0)\) étant strictement négatif et\( f(1)\) strictement positif, la solution réelle \(\alpha\) se trouve entre 0 et 1.
En utilisant le tableau de valeurs donné par une calculatrice :
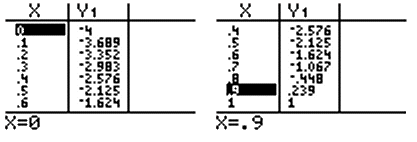
\(\alpha\) a pour valeur approchée \( 0,8\) à \(10^{-1}\) près (ou \(\alpha\) a pour valeur approchée \(0,9\) à \(10^{-1}\) près).