Trouver la limite d'une somme, d'un produit
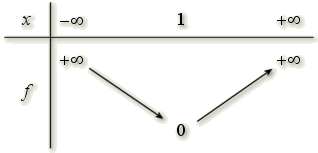
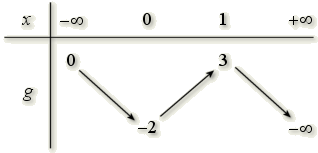
On considère les fonctions \(f\) et \(g\) définies sur \( \mathbb R\), dont les tableaux de variations sont donnés ci-dessous.
Question
Déterminer, si c'est possible,
\(\displaystyle \lim_{-\infty} f + g\)
Le résultat final
\(\displaystyle \lim_{-\infty}f+g=+\infty\)
Solution détaillée
\(\displaystyle \lim_{-\infty} f=+{\infty} \) et \(\displaystyle \lim_{-\infty} g = 0\), donc \(\displaystyle \lim_{-\infty}f+g=+\infty\).
Question
Déterminer, si c'est possible,
\(\displaystyle \lim_{1}f+g\)
Le résultat final
\(\displaystyle \lim_{1}f+g=3\)
Solution détaillée
\(\displaystyle \lim_{1}f=0\) et \(\displaystyle \lim_{1}g=3\), donc \(\displaystyle \lim_1 f+g=0+3=3 \).
Question
Déterminer, si c'est possible,
\(\displaystyle \lim_{+\infty}f+g\)
Le résultat final
On ne peut pas conclure sur
\(\displaystyle \lim_{+\infty}f+g\)
Solution détaillée
\(\displaystyle \lim_{+\infty} f=+{\infty} \) et \(\displaystyle \lim_{+\infty}g=-\infty\), les propriétés ne permettent pas de conclure directement en ce qui concerne la limite de \(f+g\) en +∞.
Question
Déterminer, si c'est possible,
\(\displaystyle \lim_{+\infty}f-g\)
Résultat final
\(\displaystyle \lim_{+\infty}f-g=+\infty\)
Solution détaillée
\(\displaystyle \lim_{+\infty} f=+{\infty} \) et \(\displaystyle \lim_{+\infty}-g=+\infty \), donc \(\displaystyle \lim_{+\infty}f-g=+\infty\).
Question
Déterminer, si c'est possible, :
\(\displaystyle \lim_{-\infty} g-f\)
Le résultat final
\(\displaystyle \lim_{-\infty}g-f=-\infty\)
Solution détaillée
\(\displaystyle \lim_{-\infty} g = 0\) et \(\displaystyle \lim_{-\infty}-f=-\infty\), donc \(\displaystyle \lim_{-\infty}g-f=-\infty\).
Question
Déterminer, si c'est possible,
\(\displaystyle \lim_{-\infty}f\times g\)
Le résultat final
On ne peut pas conclure quant à
\(\displaystyle \lim_{-\infty}f\times g\)
Solution détaillée
\(\displaystyle \lim_{-\infty} f=+{\infty} \) et \(\displaystyle \lim_{-\infty} g = 0\), les propriétés ne permettent pas de conclure directement en ce qui concerne la limite de \(f x g\) en \(-\infty\).
Question
Déterminer, si c'est possible,
\(\displaystyle \lim_{+\infty}f\times g\)
Le résultat final
\(\displaystyle \lim_{+\infty} f\times g=-\infty \)
Solution détaillée
\(\displaystyle \lim_{+\infty} f=+{\infty} \)et \(\displaystyle \lim_{+\infty}g=-\infty\), donc \(\displaystyle \lim_{+\infty} f\times g=-\infty \).
Question
Déterminer, si c'est possible,
\(\displaystyle \lim_{1}f\times g\)
Le résultat final
\(\displaystyle \lim_{1}f\times g=0\)
Solution détaillée
\(\displaystyle \lim_{1}f=0\) et \(\displaystyle \lim_{1}g=3\), donc \(\displaystyle \lim_1 f\times g=0\times 3=0 \).