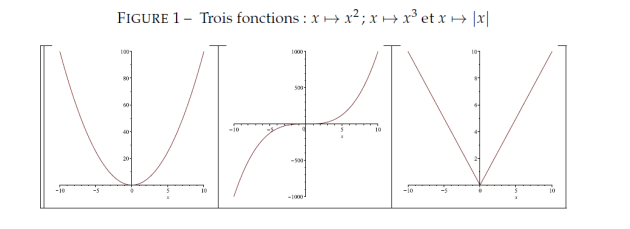
Domaine de définition
Supposons qu'une fonction \(f\) soit donnée par une expression de l'image \(f (x)\) d'un quelconque nombre \(x\). On appelle domaine de définition de la fonction \(f\) l'ensemble des nombres réels \(x\) tels que l'expression \(f (x)\) soit un nombre réel.
Pour déterminer le domaine de définition d'une fonction \(f\), on aura à appliquer des règles telles que les suivantes :
Le quotient \(a/b\) de deux nombres réels est défini si \(b\neq0\).
La racine carrée \(\sqrt{a}\) d'un nombre réel \(a\) est définie si \(a\geq0\).
Le lograithme \(ln(a)\) d'un nombre réel \(a\) est défini si \(a > 0\).
Exemple : Exemples de domaines de définition
La fonction \(f\) telle que \(f(x)=\cfrac{x^2 + 1}{x(x-1)}\) a pour domaine de définition \(\mathbb{R} \backslash \{ 0,1 \} =]-\infty, 0[\cup]0, 1[\cup]1,+\infty[\)
La fonction \(g\) telle que \(g(x)=\sqrt{x(x+1)}\) a pour domaine de définition \(]-\infty,-1]\cup[0,+\infty[\)
La fonction \(h\) telle que \(h(x)=ln(x(x+1))\) a pour domaine de définition \(]-\infty,-1[\cup]0,+\infty[\)
La courbe représentative (ou représentation graphique) d'une fonction \(f\) définie sur \(D\) est l'ensemble des points du plan de coordonnées \((x, y)\) telles que \(x \in D\) et \(y = f (x)\).
Exemples de représentation graphique
