Calculs d'intégrales à l'aide de la définition - valeur moyenne
Question
Calculer, à l'aide de la définition de l'intégrale :
\(C=\displaystyle \int_{2}^{4}\left(t-2\right)\mathrm{d}t\)
Solution détaillée
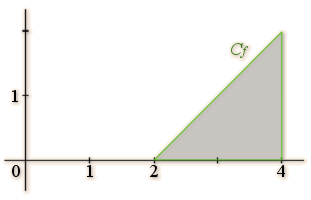
Soit \(D\) la partie du plan délimitée par la courbe de la fonction \(f:x\mapsto x-2\), l'axe des abscisses et les droites d'équation \(x = 2\) et \(x = 4\).
La fonction \(f\) est continue positive sur\( [2,4]\).
L'aire \(C\) en unités d'aire de \(D\) est l'aire du domaine délimité par un triangle rectangle soit : \( C = \frac12 base \times hauteur = \frac12 \times 2 \times 2 = 2 \).
Question
Calculer la valeur moyenne de \(x\mapsto 3\sin x\) sur \([0;\pi]\).
Solution détaillée
La fonction \(x\mapsto 3\sin x\) est continue sur \([0;\pi]\), donc la valeur moyenne de la fonction \(x\mapsto 3\sin x\) sur \([0;\pi]\) est :
\( \mu = \displaystyle \dfrac{ \displaystyle \int_{0}^{\pi}3\sin x \, \mathrm{d}x}{\pi-0} = \dfrac{3\Big[-\cos x\Big ]_{0}^{\pi}}{\pi} = \dfrac6{\pi}\).