Dérivée et extrema
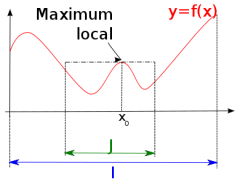
Définition : Extrema locaux d'une fonction numérique à variable réelle.
Soit \(x_0\) un nombre réel et soit \(f\) une fonction numérique à variable réelle définie sur un intervalle \(I\) contenant \(x_0\). On dit que \(f\) possède un extremum local en \(x_0\) si il existe un intervalle \(J\), inclus dans \( I\) et contenant \(x_0\) tel que l'une des deux proprietés ci-dessous soit vraie
pour tout \(x \in J\), \(f(x) \geq f(x_0)\) et dans ce cas on dit que \(f\) possède un minimum local en \(x_0\)
pour tout \(x \in J\), \(f(x) \leq f(x_0)\) et dans ce cas on dit que \(f\) possède un maximum local en \(x_0\)
un exemple du tracé d'une fonction présentant en maximum local.
Théorème : Condition suffisante d'extrema
Soit \(f\) une fonction dérivable sur un intervalle \(I\). Si \(f\) possède un extremum local en \(x_0\) alors \( f'(x_0) = 0\).
Remarque :
Si \(f\) une fonction dérivable sur un intervalle \(I\), telle qu'il existe \(x_0\in I \) avec \( f'(x_0) = 0\) alors \(f\) ne possède pas forcement un extremum local en \(x_0\). La fonction cube est dans ce cas, sa dérivée s'annule en \(0\) et pourtant cette fonction ne présente pas d'extremum en \(0\), puisqu'elle est strictement croissante sur \( \mathbb R\).
Méthode : Recherche d'extrema
Soit \(f\) une fonction à variable réelle définie sur un intervalle \(I\). Pour déterminer les nombres réels \(x_0\) en lesquels la fonction présente des extrema on procède de la manière suivante :
On repère les points où la fonction n'est pas dérivable et on étudie ces points.
Pour les points ou la fonction est dérivable : on cherche les valeurs \(x_0\) telle que\( f'(x_0) = 0\).
Pour ces valeurs \(x_0\) : si la fonction dérivée change de signe alors ce point correspond à un extremum local
si la dérivée est négative avant ce point (f décroissante) puis positive après (f croissante) alors il s'agit d'un minimum local.
si la dérivée est positive avant ce point (f croissante) puis négative après (f décroissante) alors il s'agit d'un maximum local.
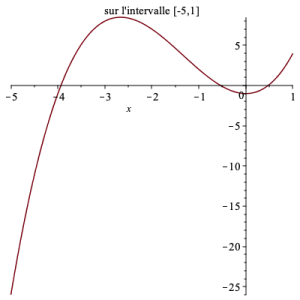
Exemple : Étude des extrema d'une fonction
Soit la fonction \(f\) donnée par \(f(x) = x^3+4x^2 -1\). Cette fonction est dérivable sur \(\mathbb R\) et sa dérivée est donnée par \(f'(x) = 3x^2+8x = x(3x+8)\) qui s'annule en \(0\) et \(-\dfrac 83\). L'étude du signe de \( f'\) nous permet de dire que
si \(x \in]-\infty\, ;\, -\dfrac 83 [\) alors \(f'(x) >0 \); si \( x \in[-\dfrac 34\, ;\, 0]\) alors \(f'(x)\leq 0\) et enfin si \(x \in]0, +\infty[\) alors \(f'(x) >0.\) La fonction \(f'\) s'annule et change de signe en \(0\) et \(-\dfrac 83.\)
Au point d'abscisse \(-\dfrac 83\) la fonction \(f\) présente un maximum et un minimum au point d'abscisse \(0\), comme indiqué sur son graphe représenté ci-contre.