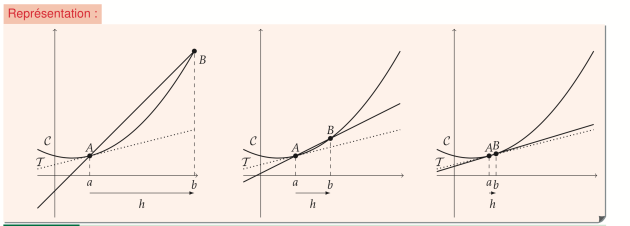
Pour une équation de la tangente à la courbe représentative d'une fonction
Définition-proposition :
Soit \(f\) une fonction définie sur un intervalle \(I\) et soit \(x_0\) appartenant à \(I\) telle que \(f\) soit dérivable en \(x_0\).
Le nombre réel \( f'(x_0)\) est appelé le nombre dérivé de \(f\) en \(x_0\), c'est le coefficient directeur de la droite tangente à la courbe représentative de \(f\) au point d'abscisse \(x_0\).
Proposition :
Soit \(f\) une fonction définie et dérivable sur un intervalle \(I\) et soit \(x_0\) appartenant à \(I\). Une équation de la tangente à la courbe représentative de \(f\) au point d'abscisse \(x_0\) est \( y = f'(x_0)(x-x_0) + f(x_0) \).
Remarque :
Si jamais la fonction \(f\) n'est pas dérivable en \(x_0\) et que l'on a \(\displaystyle \lim{x\rightarrow x_0} { \dfrac{f(x)-f(x_0)}{x-x_0}} = \pm \infty\) alors la tangente à la courbe représentative de \(f\) au point d'abscisse \(x_0 \) est verticale d'équation \(x = x_0.\)