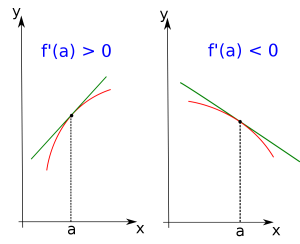
Dérivée et sens de variation
Théorème :
Soit \(f\) une fonction dérivable sur un intervalle \(I\).
Si \(f'\) est nulle sur \(I\), alors \(f\) est constante sur \(I\).
Si \(f'\) est strictement positive sur \(I\), sauf en des points isolés, alors \(f\) est strictement croissante sur \(I\).
Si \(f'\) est strictement négative sur \(I\), sauf en des points isolés, alors \(f\) est strictement décroissante sur \(I\).
Exemple : Sens de variation de la fonction cube
La fonction \(x\mapsto x^{3}\) est dérivable sur \( \mathbb R\) et sa dérivée \(x\mapsto 3x^{2}\) est strictement positive sur \( \mathbb R^{+*}.\)
On en déduit que la fonction cube est strictement croissante sur \( \mathbb R\).