Dérivation des fonctions numériques d'une variable réelle

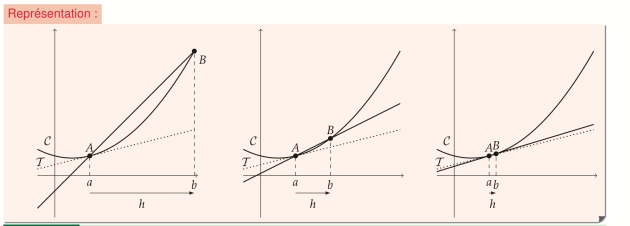
Soit \(f\) une fonction définie sur un intervalle \(I\) et soit \(x_0\) appartenant à \(I\).

\(f\) est dérivable en \(x_0\) si \(\displaystyle\lim_{x\to x_{0}}\dfrac{f\left(x\right)-f\left(x_{0}\right)}{x-x_{0}}\) existe et appartient à \(\mathbb R\).

On notera alors \( f'\left( x_0\right) = \displaystyle \lim_{x \to x_0} \dfrac{f\left( x \right) - f \left( x_0\right) }{x - x_0} = \lim_{h \to 0 } \dfrac{f\left( x_0 + h \right) - f\left( x_0\right) }h \).

Le nombre réel \( f'(x_0)\) est appelé le nombre dérivé de \(f\) en \(x_0\), c'est le coefficient directeur de la droite tangente à la courbe représentative de \(f\) au point d'abscisse \(x_0\).

Soit \(f\) une fonction définie sur un intervalle \(I\). La fonction \(f\) est dérivable sur \(I\) si \(f\) est dérivable en tout \(x_0\) de \(I\).

La fonction dérivée de \(f\) est la fonction numérique de la même variable que \( f\), qui à \(x\) associe\( f'(x)\). On la note \(f'\).