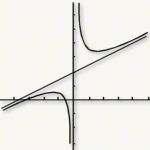
Déterminer et tracer l'asymptote d'une courbe
Soit \(f\) la fonction définie pour \(x\) différent de \(0\) par : \(f\left(x\right)=\dfrac{x^{2}+4x+2}{2x}\).
Question
Démontrer que pour tout réel \(x\) différent de \(0\), on peut écrire : \(f\left(x\right)=\dfrac12x+2+\dfrac1x\).
Solution détaillée
Pour \(x\) différent de 0, on peut écrire :
\(\displaystyle \dfrac{1}{2}x+2+\dfrac{1}{x}=\dfrac{x^{2}}{2x}+\frac{4x}{2x}+\dfrac{2}{2x}=\dfrac{x^{2}+4x+2}{2x}=f\left(x\right)\)
Question
En déduire qu'il existe une droite \(D\) asymptote à la courbe représentative de \(f\) en \(-\infty\) et \(+\infty\).
Solution détaillée
\(f(x)\) s'écrit sous la forme :
\(f\left(x\right)=\dfrac12x+2+\dfrac1x\) avec \( \displaystyle \lim_{x \to - \infty }\dfrac1x = 0 \)et \( \displaystyle \lim_{x \to + \infty }\dfrac1x = 0 \).
La droite \(D\) d'équation \( y = \dfrac12 x + 2 \) est donc asymptote à la courbe \((C)\) de \(f\) au voisinage de \(-\infty\) et au voisinage de \(+\infty\).
Question
En utilisant une calculatrice, tracer la droite \(D\) et la représentation graphique de \(f\).