Conjecturer: les limites d'une fonction en l'infini
Partie : Un premier atelier
On considère la fonction \(f\) définie pour \(x \in \mathbb R^*\), par \( f\left( x \right) = \dfrac{\sqrt{ x^2 + 1} }x \).
Question
Conjecturer, à partir de la courbe représentative de \(f\) donnée par une calculatrice, la limite de \(f\) en \(+\infty\) et la limite de \(f\) en \(-\infty\) .
Solution détaillée
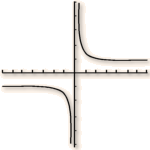
D'après la courbe représentative de \(f\), on peut penser que : \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=1\) et \(\displaystyle \lim_{x\rightarrow-\infty} f\left(x\right)=-1\).
Question
Donner des valeurs approchées de :
\(f(100)\) ; \(f(1000)\) ;\( f(12856)\)
\(f(-100)\) ; \(f(-8523)\) ; \(f(-15712)\)
Ces valeurs sont-elles conformes à la conjecture faite ?
Solution détaillée
Une calculatrice donne :
\(f(100)\approx1,00005\) ; \(f(1000)\approx1,0000005\) ; \(f(12856)\approx1,000000003\)
Lorsque \(x\) est grand, les valeurs de \(f(x)\) obtenues sont proches de \(1\).
Les résultats sont conformes à la conjecture \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=1\).
\(f(-100)\approx-1,00005\) ; \(f(-8523)\approx-1,000000007\) ; \(f(-15712)\approx1,000000002\)
Lorsque \(x\) négatif et assez grand en valeur absolue, les valeurs de \(f(x)\) obtenues sont proches de -1.
Les résultats sont conformes à la conjecture \(\displaystyle \lim_{x\rightarrow-\infty} f\left(x\right)=-1\).
Question
Justifier que pour \(x\neq 0 \), on a \( f \left( x \right) = \dfrac{\lvert x \rvert }x \sqrt{1 + \dfrac1{x^2} } \).
Que peut-on en déduire pour les limites de \(f\) en \(+\infty\) et en \(-\infty\) ?
Solution détaillée
Pour \(x\neq 0 \), on peut écrire :
\(f\left(x\right)=\dfrac{\sqrt{x^{2}+1}}x= \dfrac{\sqrt{x^{2}\left(1+\displaystyle \frac{1}{x^{2}}\right)}}{x} = \dfrac{\sqrt{x^{2}}}x \sqrt{1+\displaystyle \frac{1}{x^{2}}} = \dfrac{\lvert x \rvert}x \sqrt{1 + \frac{1}{x^{2}}} \)
Lorsque \(x\) est strictement positif, on a \(\dfrac{|x|}{x}=\dfrac{x}{x}=1\), et de plus \(\displaystyle\lim_{x\rightarrow+\infty}\sqrt{{1}+\dfrac{1}{x^{2}}}=1 \), donc \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=1\).
Lorsque \(x\) est strictement négatif, on a \(\frac{|x|}{x}=\dfrac{-x}{x}=-1\), et de plus \(\displaystyle\lim_{x\rightarrow-\infty}{\sqrt{{1}+\frac{1}{x^{2}}}}=1\), donc \(\displaystyle \lim_{x\rightarrow-\infty} f\left(x\right)=-1\).
Partie : Un deuxième atelier qui utilise la définition de la limite.
On considère la fonction \(f\) définie pour \(x>0\), par : \(f\left(x\right)=\displaystyle \dfrac{x+\sqrt{x}}{2}\).
Question
Conjecturer, à partir de la courbe représentative de \(f\) donnée par une calculatrice, la limite de \(f\) en \(+\infty\).
Solution détaillée
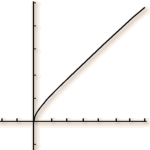
D'après la courbe représentative de \(f\), on peut penser que : \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=+\infty \).
Question
Donner des valeurs approchées de : \(f\)(10) ; \(f\)(100) ; \(f\)(1000) ; \(f\)(12823).
Ces valeurs sont-elles conformes à la conjecture faite ?
Solution détaillée
\(f(10)\approx 6,58\) ; \(f(100)= 55\) ; \(f(1000)\approx 516\) ; \(f(12823)\approx 6468\).
Il semble que l'on puisse obtenir des valeurs de \(f(x)\) aussi grandes que l'on veut en prenant des valeurs de \(x\) suffisamment grandes.
Ceci est conforme à la conjecture \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=+\infty \).
Question
Justifier que pour tout \(x>0\), \(f\left(x\right)>\dfrac{x}2\).
En déduire que pour tout réel \(A\), il existe un réel \(\beta\) tel que : si \(x>\beta\) alors\(f(x)>A\).
Que peut-on en déduire ?
Solution détaillée
On sait que pour tout réel \(x\) strictement positif, on a \(\sqrt{x}>0\).
On en déduit que : \(x+\sqrt{x}>x\) et par conséquent \(f\left(x\right)>\dfrac{x}2\). On en poursuivre le raisonnement de deux manières :
1) Soit \(A\) un nombre réel, considérons le réel \(\beta=2A\).
Alors si \(x>\beta\), on a \(\dfrac{x}{2}>{A}\) et par conséquent \(f(x)>A\).
On peut en déduire que tout intervalle \(I\) du type \(]A ; +\infty[\) contient toutes les valeurs \(f(x)\) pour \(x\) assez grand \((x>2A)\), donc \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=+\infty \).
2) On peut aussi conclure en utilisant les résultats de comparaison sur les limites qui permettent de dire que puisque \( \displaystyle \lim_{x \rightarrow +\infty} {\dfrac{x}2} = +\infty\) et que \(f\left(x\right)>\dfrac{x}2\), on a \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=+\infty \).