Limites en un réel a
Définition : Limite l en a
Soit \(a\) un nombre réel et soit une fonction \(f\) définie sur un intervalle centré en \(a\), mais ne contenant pas nécessairement \(a\). Dire que la fonction \(f\) tend vers le nombre réel \(\ell\) quand \(x\) tend vers \(a\) signifie que quelque soit l'intervalle ouvert \(I\) contenant \(\ell\) , cet intervalle \(I\) contient toutes les valeurs \(f(x)\) pour \(x\) assez proche de \(a\).
On écrira : \(\displaystyle\lim_{x\rightarrow a} f\left(x\right)=\ell\) ou \(\displaystyle \lim_{a}f=\ell\).
Limites à droite et à gauche
On parle de limite à droite en \(a\), si la fonction est définie sur un intervalle de la forme \(]a\, ; \, a +\eta[\) où \(\eta\) est un nombre réel positif et si \(x\) est assez proche de \(a\) en restant supérieur à \(a\). Si la fonction est notée \(f\), cette limite se note \(\displaystyle \lim_{x \rightarrow a^+}{f(x)}.\)
On parle de limite à gauche en \(a\), si la fonction est définie sur un intervalle de la forme \( ]a-\eta\, ; \, a[\) où \(\eta\) est un nombre réel positif et si \(x\) est assez proche de \(a\) en restant inférieur à \(a\). Si la fonction est notée \(f\), cette limite se note \(\displaystyle \lim_{x \rightarrow a^- }{f(x)}.\)
Si la limite d'une fonction existe en un point, elle sera la même à droite et à gauche en ce point et réciproquement une fonction aura une limite en un point si elle a à la fois une limite à droite et à gauche de ce point, les deux limites étant les mêmes. Ceci est encore valable lorsque les limites sont infinies et de même signe.
Exemple : Graphiquement on peut avoir :
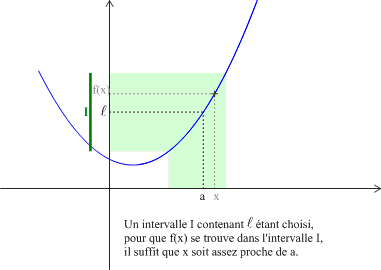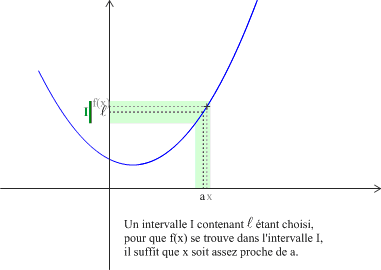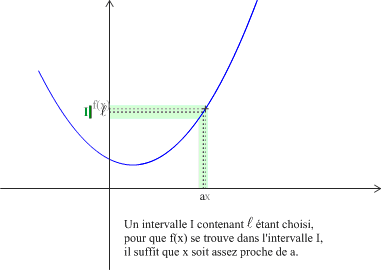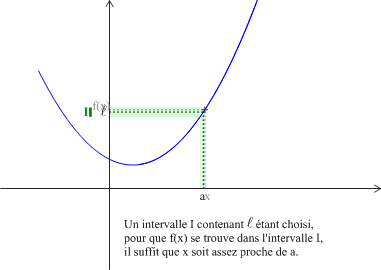
Définition : Limite +∞ en a
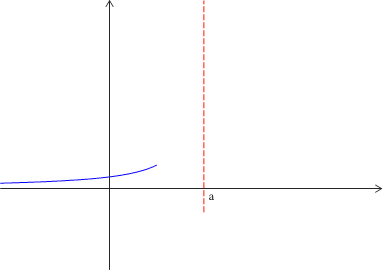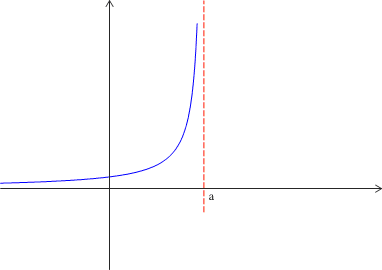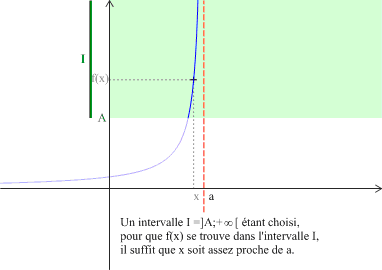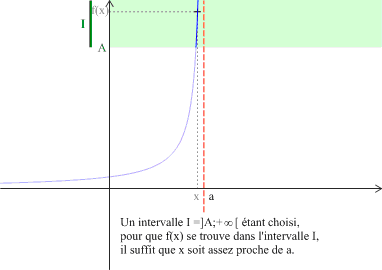
Soit \(a\) un nombre réel et soit une fonction \(f\) définie sur un intervalle centré en \(a\), mais ne contenant pas nécessairement \(a\). Dire que la fonction \(f\) tend vers \(+\infty\) quand \(x\) tend vers \(a\) signifie que tout intervalle \(I\) du type \(]A ;+\infty[\) contient toutes les valeurs \(f(x)\) pour \(x\) assez proche de \(a\).
On écrira : \(\displaystyle \lim_{x \to a}f\left(x\right)=+\infty\) ou \(\displaystyle \lim_{a}f=+\infty\).
On dit alors que la droite (parallèle à l'axe des ordonnées) d'équation \(x=a\) est asymptote à la courbe \((C)\) de \(f\).
Exemple : Ici lorsque x tend vers a en restant inférieur à a ( limite à gauche)
Définition : Limite -∞ en a
Soit \(a\) un nombre réel et soit une fonction \(f\) définie sur un intervalle centré en \(a\), mais ne contenant pas nécessairement \(a\). Dire que la fonction \(f\) tend vers \(-\infty\) quand \(x\) tend vers \(a\) signifie que tout intervalle du type \(] -\infty ; A[\) contient toutes les valeurs \(f(x)\) pour \(x\) assez proche de \(a\).
On écrira : \(\displaystyle \lim_{x\rightarrow a} f\left(x\right)=-\infty \)ou \(\displaystyle \lim_{a}f=-\infty\).
On dit alors que la droite (parallèle à l'axe des ordonnées) d'équation \(x=a\) est asymptote à la courbe \((C)\) de \(f\).