Asymptote oblique
Nous avons introduit au paragraphe précédent la notion d'asymptote parallèle à l'axe des abscisses (horizontales si le repère est orthonormé). Elles existent dans le cas où la limite de la fonction est un nombre réel lorsque la variable tend vers l'infini.
Il peut exister également des asymptotes dans d'autres cas en particulier lorsque la fonction tend vers l'infini en l'infini. Ce sont ces définitions que nous introduisons ici.
Définition : Asymptote oblique en +∞
Soit \(\alpha\) un nombre réel positif. Soit \(f\) une fonction définie sur \(]\alpha ;+\infty[\).
S'il existe deux réels \(a\) et \(b\) et une fonction \(g\) tels que :
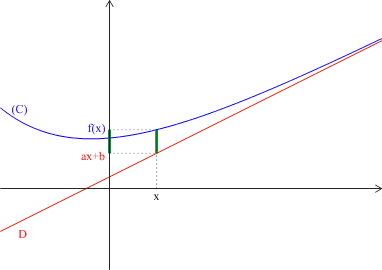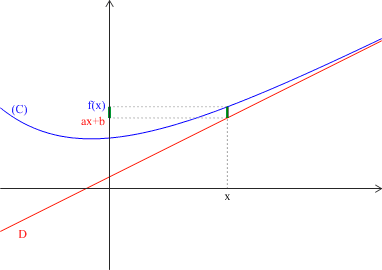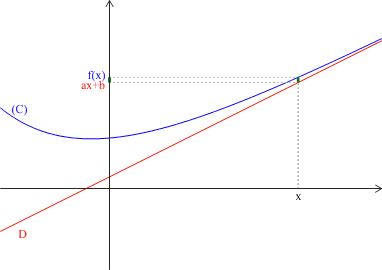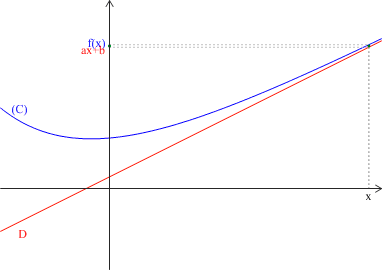
pour tout \(x\) dans \(]\alpha ;+\infty[\), \(f(x)=ax+b+g(x)\) et \(\displaystyle \lim_{x\rightarrow+\infty} g\left(x\right)=0 \),
alors la droite \(D\) d'équation \(y=ax+b\) est asymptote à la courbe \((C)\) de \(f\) au voisinage de \(+\infty\).
Remarque :
On remarque que nécessairement, dans ce cas, la limite de la fonction en \(+\infty\) est \(\pm\infty\).
Exemple :
Définition : Asymptote oblique en -∞
Soit \(\alpha\) un nombre réel négatif. Soit \(f\) une fonction définie sur \(]-\infty ;\, \alpha[\).
S'il existe deux réels \(a\) et \(b\) et une fonction \(g\) tels que :
pour tout \(x\) dans \(]-\infty ;\alpha[\), \(f(x)=ax+b+g(x)\) et \(\displaystyle \lim_{x \to -\infty} g\left(x\right)=0\),
alors la droite \(D\) d'équation \(y=ax+b\) est asymptote à la courbe \((C)\) de \(f\) au voisinage de \(-\infty\).
Remarque :
On remarque que nécessairement dans ce cas, la limite de la fonction en \(-\infty\) est \(\pm \infty\).