Limites en l'infini
Définition : Limite l en +∞
Soit \(\alpha\) un nombre réel. Dire qu'une fonction \(f\), définie sur \(]\alpha\, ;\, +\infty[\), tend vers le nombre réel \(\ell\) quand \(x\) tend vers \(+\infty\) signifie que quelque soit l'intervalle ouvert \(I\) contenant \(\ell\), cet intervalle \(I\) contient toutes les valeurs \(f(x)\) pour \(x\) assez grand.
On écrira : \(\displaystyle \lim_{+\infty} f=\ell\) ou \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=\ell\).
On dit alors que la droite (parallèle à l'axe des abscisses) d'équation \(y=\ell\) est asymptote à la courbe \((C)\) de \(f\) au voisinage de \(+\infty\).
Exemple : Graphiquement

Exemple : Quelques fonctions dans ce cas
La fonction \(x \mapsto \dfrac 1 x\) tend vers 0 lorsque \(x\) tend vers l'infini. De même que la fonction \( x \mapsto \dfrac {1}{x^2 } \) ou encore \( x \mapsto \dfrac{1}{x^2 + x}\) .
De manière analogue la fonction \( x \mapsto 2 + \dfrac 1 x\) tend vers \(2\) quand \(x\) vers \(+ \infty.\)
Exemple : Ou encore graphiquement cas d'une fonction qui tend vers une valeur fini en l'infini en décroissant.

Définition : Limite l en - ∞
Soit \(\alpha\) un nombre réel. Dire qu'une fonction \(f\), définie sur \(]-\infty \,;\,\alpha[\), tend vers le nombre réel \(\ell\) quand \(x\) tend vers \(-\infty\) signifie que quelque soit l'intervalle ouvert \(I\) contenant \(\ell\), cet intervalle \(I\) contient toutes les valeurs \(f(x)\) pour \(x\) négatif et assez grand en valeur absolue.
On écrira : \(\displaystyle \lim_{x\rightarrow-\infty} f\left(x\right)=\ell\) ou \(\displaystyle \lim_{-\infty} f=\ell \).
On dit alors que la droite (parallèle à l'axe des abscisses) d'équation \(y\)= \(\ell\) est asymptote à la courbe \((C)\) de \(f\) au voisinage de \(-\infty\).
Exemple :

Exemple : Quelques fonctions dans ce cas
La fonction \(x \mapsto \dfrac 1 x\) tend vers 0 lorsque \(x\) tend vers \(-\infty\). De même que la fonction \( x \mapsto \dfrac {-1}{ x^2} \) ou encore \( x \mapsto \dfrac{1}{x^2 + x}\) .
De manière analogue la fonction \( x \mapsto 2 + \dfrac 1 x\) tend vers \(2\) quand \(x\) vers \(- \infty.\)
Définition : Limite +∞ en +∞
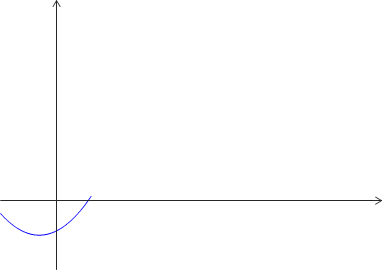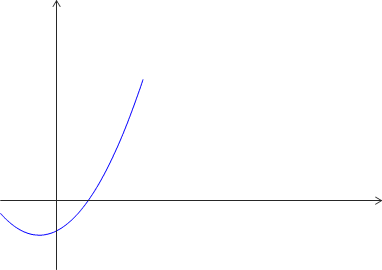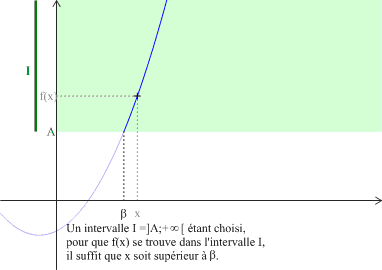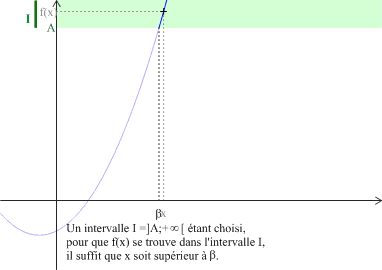
Soit \(\alpha\) un nombre réel. Dire qu'une fonction \(f\), définie sur \(]\alpha ;+\infty[\), tend vers \(+\infty\) quand \(x\) tend vers \(+\infty\) signifie que tout intervalle \(I\) du type \(]A ;+\infty[\) contient toutes les valeurs \(f(x)\) pour \(x\) assez grand.
On écrira : \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=+\infty \) ou \(\displaystyle \lim_{+\infty} f=+\infty\).
Exemple : Un exemple graphique avec une croissance monotone en l'infini.
Exemple :
Si on considère la fonction \(x \mapsto x^2\) , elle tend vers \(+\infty\) quand \(x\) tend vers \(+\infty\). C'est aussi le cas de la fonction \(x \mapsto \sqrt x\) ou encore de \(x \mapsto x^2-x\).
Définition : Limite +∞ en -∞
Soit \(\alpha\) un nombre réel. Dire qu'une fonction \(f\), définie sur \(]-\infty;\alpha [\) , tend vers \(+\infty\) quand \(x\) tend vers \(-\infty\) signifie que tout intervalle \(I\) du type \(]A ;+\infty[\) contient toutes les valeurs \(f(x)\) pour \(x\) négatif et assez grand en valeur absolue.
On écrira : \(\displaystyle \lim_{x\rightarrow-\infty} f\left(x\right)=+\infty \) ou \(\displaystyle \lim_{-\infty} f=+\infty\).
Définition : Limite -∞ en +∞
Soit \(\alpha\) un nombre réel. Dire qu'une fonction \(f\), définie sur \(]\alpha ;+\infty[\), tend vers \(-\infty\) quand \(x\) tend vers \(+\infty\) signifie que tout intervalle \(I\) du type \(]-\infty ;A[\) contient toutes les valeurs \(f(x)\) pour \(x\) assez grand.
On écrira : \(\displaystyle \lim_{x\rightarrow+\infty} f\left(x\right)=-\infty \) ou \(\displaystyle \lim_{+\infty} f=-\infty \).
Définition : Limite -∞ en -∞
Soit \(\alpha\) un nombre réel. Dire qu'une fonction \(f\), définie sur \(]-\infty ; \alpha[\), tend vers \(-\infty\) quand \(x\) tend vers \(-\infty\) signifie que tout intervalle \(I\) du type \(]-\infty ; A[\) contient toutes les valeurs \(f(x)\) pour \(x\) négatif et assez grand en valeur absolue.
On écrira : \(\displaystyle \lim_{x\rightarrow-\infty} f\left(x\right)=-\infty \) ou \(\displaystyle \lim_{-\infty} f=-\infty \).
Exemple :
C'est le cas des fonctions suivantes : \(x \mapsto x^3\) ou \(x \mapsto -x^2\) .