Valeurs intermédiaires
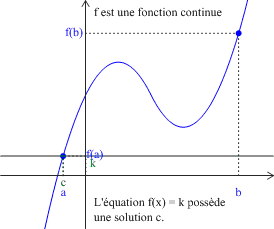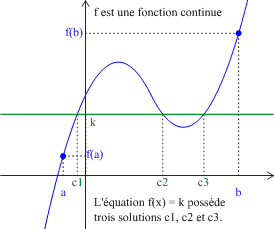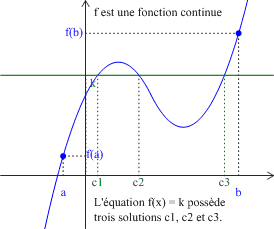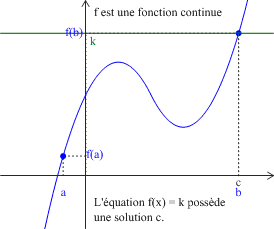
Théorème : Théorème des valeurs intermédiaires
Soit \(f\) une fonction définie et continue sur un intervalle \(I\), soit \(a\in{I}\) et \(b\in{I}\).
Pour tout nombre réel \(k\) compris entre \(f(a)\) et \(f(b)\), il existe au moins un réel \(c\) compris entre \(a\) et \(b\) tel que \(f(c)=k\) (c'est-à-dire : l'équation \(f(x)=k\) a au moins une solution comprise entre \(a\) et \(b\)).
Exemple :
Corollaire :
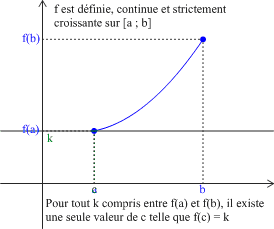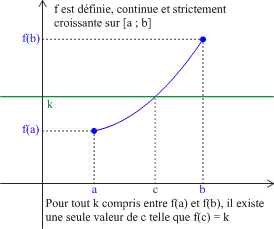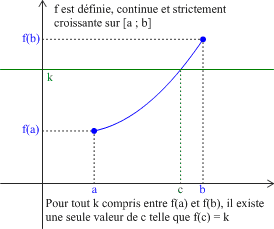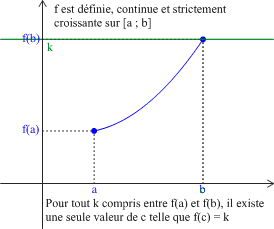
Soit \(f\) une fonction définie, continue et strictement monotone sur un intervalle \([a ; b]\).
Pour tout nombre réel \(k\) compris entre \(f(a)\) et \(f(b)\), il existe un et un seul réel \(c\) dans l'intervalle \([a ;b]\) tel que \(f(c)=k\) (c'est-à-dire : l'équation \(f(x)=k\) a une solution unique dans l'intervalle \([a ;b]\)).
Exemple :
Corollaire : Extension du corollaire
Le résultat de ce corollaire peut être étendu à une fonction définie continue et strictement monotone sur un intervalle ouvert et/ou non borné en faisant appel aux limites de la fonction \(f\).
Exemple :
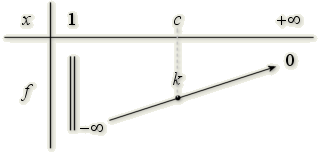
Soit \(f\) une fonction ayant le tableau de variation ci-dessous.
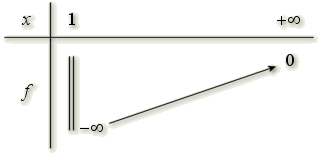
On peut déduire de ce tableau de variation que pour tout nombre réel \(k\) dans l'intervalle \(]-\infty;0[\) , l'équation \(f(x)=k\) a une solution unique \(c\) dans \(]1;+\infty[\).