Continuité
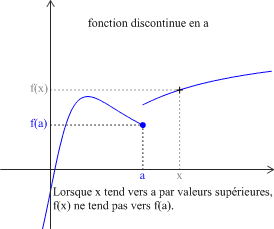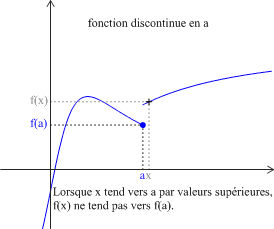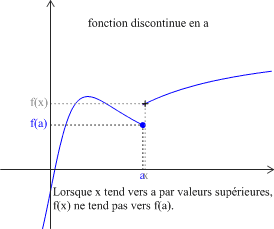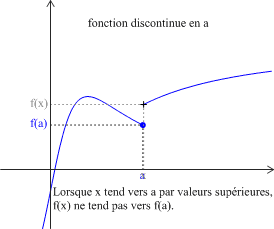
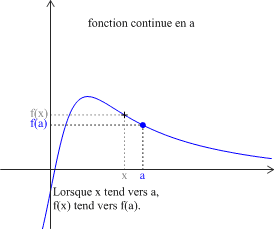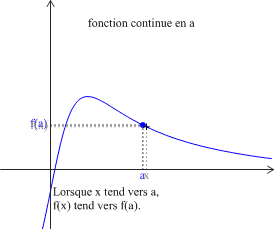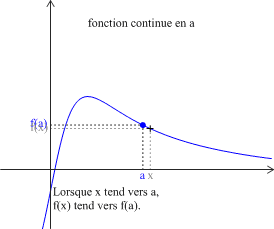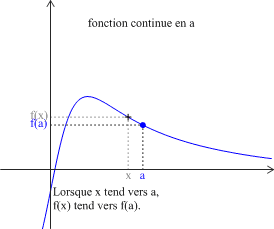
Définition : Fonction continue en a
Soit \(f\) une fonction définie sur un intervalle \(I\) et soit \(a\in{I}\).
\(f\) est continue en \(a\) si \(\displaystyle \lim_{x\rightarrow a} f\left(x\right)=f\left(a\right) \) (ou encore \(\displaystyle \lim_{h\rightarrow 0 } f\left(a+h\right)=f\left(a\right) \)).
Définition : Fonction continue sur un intervalle
Soit \(f\) une fonction définie sur un intervalle \(I\).
\(f\) est continue sur \(I\) si \(f\) est continue en tout \(a\in{I}\).
Définition : Courbe d'une fonction continue
Lorsqu'une fonction est continue sur un intervalle \(I\), sa courbe représentative sur \(I\) peut être tracée sans lever le crayon de la feuille.
Exemple :
Exemple :