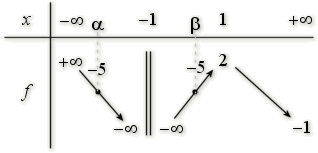Déterminer le nombre de solutions d'une équation
Soit \(f\) une fonction continue sur \(\mathbb R\) ayant pour tableau de variations :
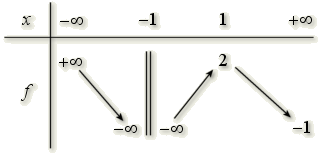
Question
Donner le nombre de solutions de l'équation suivante :
\(f(x)=0\)
Solution détaillée
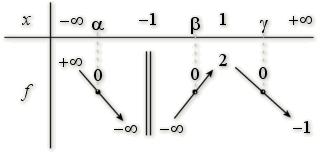
\(0\) appartient à chacun des intervalles \(]-\infty;+\infty[\) ; \(]-\infty;2[\) et \(]-1;2\)[.
D'après le tableau de variations, l'équation \(f(x)=0\) a donc trois solutions.
Question
Donner le nombre de solutions réelles de l'équation
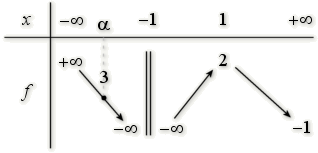
\(f(x)=3\)
Solution détaillée
\(3\) appartient à l'intervalle \(]-\infty;+\infty[\), mais n'appartient pas aux intervalles \(]-∞;2[ \) et \(]-1 ;2[\).
D'après le tableau de variations, l'équation \(f(x)=3\) a donc une solution réelle.
Question
Donner le nombre de solutions réelle de l'équation
\(f(x)=-5\)
Solution détaillée
\(-5\) appartient à l'intervalle \(]-\infty ;+\infty[\) ainsi qu'à l'intervalle \(]-\infty ;2[\) mais n'appartient pas à l'intervalle \(]-1;2[\).
D'après le tableau de variations, l'équation \(f(x)=-5\) a donc deux solutions réelles.